JEE Main Online Computer Based Test (CBT) Examination Afternoon Held on 15-04-2018,
PHYSICS
1. The characteristic distance at which quantum gravitational effects are significant, the Planck length, can be determined from a suitable combination of the fundamental physical constants G, h and c. Which of the following correctly gives the Planck length ?
(1) G h2 c3
(2) G2 h c
(3) G1/2 h2 c
(4) 
2. A man in a car at location Q on a straight highway is moving with speed υ. He decides to reach a point P in a field at a distance d from the highway (point M) as shown in the figure. Speed of the car in the field is half to that on the highway. What should be the distance RM, so that the time taken to reach P is minimum ?
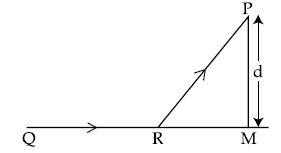
(1) d
(2) d/√2
(3) d/2
(4) d/√3
3. A body of mass 2 kg slides down with an acceleration of 3 m/s2 on a rough inclined plane having a slope of 30°. The external force required to take the same body up the plane with the same acceleration will be : (g=10 m/s2)
(1) 14 N
(2) 20 N
(3) 6 N
(4) 4 N
4. A proton of mass m collides elastically with a particle of unknown mass at rest. After the collision, the proton and the unknown particle are seen moving at an angle of 90° with respect to each other. The mass of unknown particle is :
(1) m/2
(2) m
(3) m/√3
(4) 2 m
5. A disc rotates about its axis of symmetry in a horizontal plane at a steady rate of 3.5 revolutions per second. A coin placed at a distance of 1.25 cm from the axis of rotation remains at rest on the disc. The coefficient of friction between the coin and the disc is : (g=10 m/s2)
(1) 0.5
(2) 0.3
(3) 0.7
(4) 0.6
6. A thin uniform bar of length L and mass 8 m lies on a smooth horizontal table. Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2υ and υ respectively. The masses stick to the bar after collision at a distance ![]() respectively from the centre of the abr. If the bar starts rotating about its center of mass as a result of collision, the angular speed of the bar will be :
respectively from the centre of the abr. If the bar starts rotating about its center of mass as a result of collision, the angular speed of the bar will be :

(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
7. A thin rod MN, free to rotate in the vertical plane about the fixed end N, is held horizontal. When the end M is released the speed of this end, when the rod makes an angle α with the horizontal, will be proportional to : (see figure)
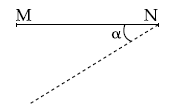
(1) ![]()
(2) sin α
(3) ![]()
(4) cos α
8. As shown in the figure, forces of 105 N each are applied in opposite directions, on the upper and lower faces of a cube of side 10 cm, shifting the upper face parallel to itself by 0.5 cm. If the side of another cube of the same material is 20 cm, then under similar conditions as above, the displacement will be :

(1) 0.25 cm
(2) 0.37 cm
(3) 0.75 cm
(4) 1.00 cm
9. When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes 5r/4. Taking the atmospheric pressure to be equal to 10 m height of water column, the depth of the lake would approximately be (ignore the surface tension and the effect of temperature) :
(1) 11.2 m
(2) 8.7 m
(3) 9.5 m
(4) 10.5 m
10. Two Carnot engines A and B are operated in series. Engine A receives heat from a reservoir at 600 K and rejects heat to a reservoir at temperature T. Engine B receives heat rejected by engine A and in turn rejects it to a reservoir at 100 K. If the efficiencies of the two engines A and B are represented by ηA and ηB, respectively, then what is the value of ![]()
(1) 12/7
(2) 7/12
(3) 12/5
(4) 5/12
11. The value closest to the thermal velocity of a Helium atom at room temperature (300 K) in ms−1 : [kB = 1.4 × 10−23 J/K; mHe = 7 × 10−27 kg]
(1) 1.3 × 104
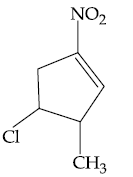
(2) 1.3 × 103
(3) 1.3× 105
(4) 1.3 × 102
12. Two simple harmonic motions, as shown below, are at right angles. They are combined to form Lissajous figures.
x(t) = A sin (at + δ)
y(t) = B sin (bt)
Identify the correct match below.
Parameters Curve
(1) A ≠ B, a = b ; δ = 0 Parabola
(2) A = B, a = b ; δ = π/2 Line
(3) A ≠ B, a = b ; δ = π/2 Ellipse
(4) A = B, a = 2b ; δ = π/2 Circle
13. 5 beats/second are heard when a tuning fork is sounded with a sonometer wire under tension, when the length of the sonometer wire is either 0.95 m or 1 m. The frequency of the fork will be :
(1) 195 Hz
(2) 150 Hz
(3) 300 Hz
(4) 251 Hz
14. A solid ball of radius R has a charge density ρ given by ρ = ρ0(1 – r/R) for 0 ≤ r ≤ The electric field outside the ball is :
(1) ![]()
(2) 
(3) 
(4) 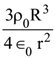
15. A parallel plate capacitor with area 200 cm2 and separation between the plates 1.5 cm, is connected across a battery of emf V. If the force of attraction between the plates is 25×10−6 N, the value of V is approximately :
(1) 250 V
(2) 100 V
(3) 300 V
(4) 150 V
16. A copper rod of cross-sectional area A carries a uniform current I through it. At temperature T, if the volume charge density of the rod is ρ, how long will the charges take to travel a distance d ?
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
17. A capacitor C1=1.0 μF is charged up to a voltage V=60 V by connecting it to battery B through switch (1). Now C1 is disconnected from battery and connected to a circuit consisting of two uncharged capacitors C2=3.0 μF and C3=6.0 μF through switch (2), as shown in the figure. The sum of final charges on C2 and C3 is :

(1) 40 μC
(2) 36 μC
(3) 20 μC
(4) 54 μC
18. A current of 1 A is flowing on the sides of an equilateral triangle of side 4.5×10−2 The magnetic field at the centre of the triangle will be :
(1) 2 ×10−5 Wb/m2
(2) Zero
(3) 8 ×10−5 Wb/m2
(4) 4 ×10−5 Wb/m2
19. At the centre of a fixed large circular coil of radius R, a much smaller circular coil of radius r is placed. The two coils are concentric and are in the same The larger coil carries a current I. The smaller coil is set to rotate with a constant angular velocity ω about an axis along their common diameter. Calculate the emf induced in the smaller coil after a time t of its start of rotation.
(1) 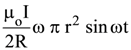
(2) 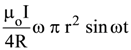
(3) 
(4) 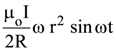
20. 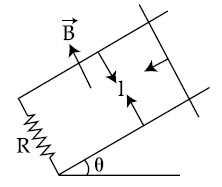
A copper rod of mass m slides under gravity on two smooth parallel rails, with
separation l and set at an angle of θ with the horizontal. At the bottom, rails are joined by a resistance R. There is a uniform magnetic field B normal to the plane of the rails, as shown in the figure. The terminal speed of the copper rod is :
(1) 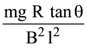
(2) 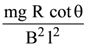
(3) 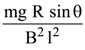
(4) 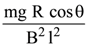
21. A plane polarized monochromatic EM wave is traveling in vacuum along z direction such that at t = t1 it is found that the electric field is zero at a spatial point z1. The next zero that occurs in its neighbourhood is at z2. The frequency of the electromagnetic wave is :
(1) 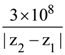
(2) 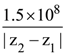
(3) 
(4) 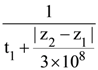
22. A convergent doublet of separated lenses, corrected for spherical aberration, has resultant focal length of 10 cm. The separation between the two lenses is 2 cm. The focal lengths of the component lenses are :
(1) 10 cm, 12 cm
(2) 12 cm, 14 cm
(3) 16 cm, 18 cm
(4) 18 cm, 20 cm
23. A plane polarized light is incident on a polariser with its pass axis making angle θ with x-axis, as shown in the figure. At four different values of θ, θ=8°, 38°, 188° and 218°, the observed intensities are same. What is the angle between the direction of polarization and x-axis ?

(1) 98°
(2) 128°
(3) 203°
(4) 45°
24. If the de Broglie wavelengths associated with a proton and an α-particle are equal, then the ratio of velocities of the proton and the α-particle will be :
(1) 4 : 1
(2) 2 : 1
(3) 1 : 2
(4) 1 : 4
25. Muon (μ−) is a negatively charged (|q| = |e|) particle with a mass mμ=200 me, where me is the mass of the electron and e is the electronic charge. If μ− is bound to a proton to form a hydrogen like atom, identify the correct statements.
(A) Radius of the muonic orbit is 200 times smaller than that of the electron.
(B) The speed of the μ− in the nth orbit is 1/200 times that of the electron in the nth orbit.
(C) The ionization energy of muonic atom is 200 times more than that of an hydrogen atom.
(D) The momentum of the muon in the nth orbit is 200 times more than that of the electron.
(1) (A), (B), (D)
(2) (A), (C), (D)
(3) (B), (D)
(4) (C), (D)
26. An unstable heavy nucleus at rest breaks into two nuclei which move away with velocities in the ratio of 8 : 27. The ratio of the radii of the nuclei (assumed to be spherical) is :
(1) 8 : 27
(2) 4 : 9
(3) 3 : 2
(4) 2 : 3
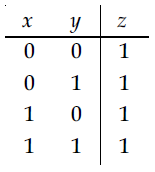
27. Truth table for the following digital circuit will be :
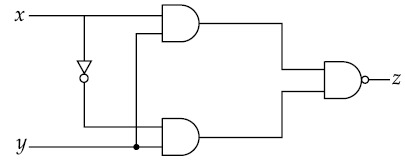
(1) 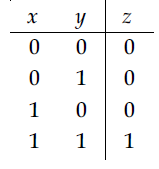
(2) 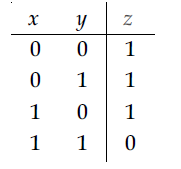
(3) 
(4) 
28. The carrier frequency of a transmitter is provided by a tank circuit of a coil of inductance 49 μH and a capacitance of 2.5 nF. It is modulated by an audio signal of 12 kHz. The frequency range occupied by the side bands is :
(1) 13482 kHz − 13494 kHz
(2) 442 kHz − 466 kHz
(3) 63 kHz − 75 kHz
(4) 18 kHz − 30 kHz
29. A constant voltage is applied between two ends of a metallic wire. If the length is halved and the radius of the wire is doubled, the rate of heat developed in the wire will be :
(1) Doubled
(2) Halved
(3) Unchanged
(4) Increased 8 times
30. A body takes 10 minutes to cool from 60°C to 50° The temperature of surroundings is constant at 25°C. Then, the temperature of the body after next 10 minutes will be approximately :
(1) 47°C
(2) 41°C
(3) 45°C
(4) 43°C
31. For per gram of reactant, the maximum quantity of N2 gas is produced in which of the following thermal decomposition reactions ?
(Given : Atomic wt. – Cr = 52 u, Ba = 137 u)
(1) (NH4)2Cr2O7(s) → N2(g)+4H2O(g) +Cr2O3(s)
(2) 2NH4NO3(s) → 2 N2(g)+4H2O(g) +O2(g)
(3) Ba(N3)2(s) → Ba(s)+3N2(g)
(4) 2NH3(g) → N2(g)+3H2(g)
32. All of the following share the same crystal structure except :
(1) LiCl
(2) NaCl
(3) RbCl
(4) CsCl
33. The de-Broglie’s wavelength of electron present in first Bohr orbit of ‘H’ atom is :
(1) 0529 Å
(2) 2π × 0.529 Å
(3) ![]()
(4) 4 × 0.529 Å
34. ∆fG° at 500 K for substance ‘S’ in liquid state and gaseous state are +100.7 kcal mol−1 and +103 kcal mol−1, respectively. Vapour pressure of liquid ‘S’ at 500 K is approximately equal to :
(R – 2 cal K−1 mol−1)
(1) 0.1 atm
(2) 1 atm
(3) 10 atm
(4) 100 atm
35. Given
(i) 2Fe2O3(s) → 4Fe(s)+3O2(g) ∆rG° = +1487.0 kJ mol−1
(ii) 2CO(g) + O2(g) → 2CO2(g); ∆rG° = −514.4 kJ mol−1
Free energy change, ∆rG° for the reaction 2Fe2O3(s) + 6CO(g) → 4Fe(s) + 6CO2(g) will be :
(1) −112.4 kJ mol−1
(2) −56.2 kJ mol−1
(3) −168.2 kJ mol−1
(4) −208.0 kJ mol−1
36. Two 5 molal solutions are prepared by dissolving a non-electrolyte non-volatile solute separately in the solvents X and Y. The molecular weights of the solvents are MX and MY, respectively where ![]() The relative lowering of vapour pressure of the solution in X is “m” times that of the solution in Y. Given that the number of moles of solute is very small in comparison to that of solvent, the value of “m” is :
The relative lowering of vapour pressure of the solution in X is “m” times that of the solution in Y. Given that the number of moles of solute is very small in comparison to that of solvent, the value of “m” is :
(1) 4/3
(2) 3/4
(3) 1/2
(4) 1/4
37. Following four solutions are prepared by mixing different volumes of NaOH and HCl of different concentrations, pH of which one of them will be equal to 1 ?
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
38. At a certain temperature in a 5 L vessel, 2 moles of carbon monoxide and 3 moles of chlorine were allowed to reach equilibrium according to the reaction,
CO + Cl2 ⇌ COCl2
At equilibrium, if one mole of CO is present then equilibrium constant (Kc) for the reaction is :
(1) 2
(2) 2.5
(3) 3
(4) 4
39. If x gram of gas is adsorbed by m gram of adsorbent at pressure P, the plot of ![]() versus log P is linear. The slope of the plot is :
versus log P is linear. The slope of the plot is :
(n and k are constants and n > 1)
(1) 2 k
(2) log k
(3) n
(4) 1/n
40. For a first order reaction, A → P, t1/2 (half-life) is 10 days. The time required for 1/4th conversion of A (in days) is :
(ln 2 = 0.693, ln 3 = 1.1)
(1) 5
(2) 3.2
(3) 4.1
(4) 2.5
41. Which of the following best describes the diagram below of a molecular orbital ?
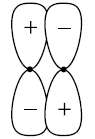
(1) A non-bonding orbital
(2) An antibonding σ orbital
(3) A bonding π orbital
(4) An antibonding π orbital
42. Biochemical Oxygen Demand (BOD) value can be a measure of water pollution caused by the organic matter. Which of the following statements is correct ?
(1) Aerobic bacteria decrease the BOD value.
(2) Anaerobic bacteria increase the BOD value.
(3) Clean water has BOD value higher than 10 ppm.
(4) Polluted water has BOD value higher than 10 ppm.
43. In KO2, the nature of oxygen species and the oxidation state of oxygen atom are, respectively :
(1) Oxide and −2
(2) Superoxide and −1/2
(3) Peroxide and −1/2
(4) Superoxide and −1
44. The number of P−O bonds in P4O6 is :
(1) 6
(2) 9
(3) 12
(4) 18
45. Lithium aluminium hydride reacts with silicon tetrachloride to form :
(1) LiCl, AlH3 and SiH4
(2) LiCl, AlCl3 and SiH4
(3) LiH, AlCl3 and SiCl2
(4) LiH, AlH3 and SiH4
46. The correct order of spin-only magnetic moments among the following is :
(Atomic number : Mn=25, Co=27, Ni=28, Zn=30)
(1) [ZnCl4]2− > [NiCl4]2− > [CoCl4]2− > [MnCl4]2−
(2) [CoCl4]2− > [MnCl4]2− > [NiCl4]2− > [ZnCl4]2−
(3) [NiCl4]2− > [CoCl4]2− > [MnCl4]2− > [ZnCl4]2−
(4) [MnCl4]2− > [CoCl4]2− > [NiCl4]2− > [ZnCl4]2−
47. The correct order of electron affinity is :
(1) F > Cl > O
(2) F > O > Cl
(3) Cl > F > O
(4) O > F > Cl
48. In XeO3F2, the number of bond pair(s), π-bond(s) and lone pair(s) on Xe atom respectively are :
(1) 5, 2, 0
(2) 4, 2, 2
(3) 5, 3, 0
(4) 4, 4, 0
49. In the leaching method, bauxite ore is digested with a concentrated solution of NaOH that produces ‘X’. When CO2 gas is passed through the aqueous solution of ‘X’, a hydrated compound ‘Y’ is precipitated. ‘X’ and ‘Y’ respectively are :
(1) NaAlO2 and Al2(CO3)3⋅ x H2O
(2) Al(OH)3 and Al2O3⋅ x H2O
(3) Na[Al(OH)4] and Al2O3⋅ x H2O
(4) Na[Al(OH)4] and Al2(CO3)3⋅ x H2O
50. The total number of possible isomers for square-planar [Pt(Cl)(NO2)(NO3)(SCN)]2− is :
(1) 8
(2) 12
(3) 16
(4) 24
51. Two compounds I and II are eluted by column chromatography (adsorption of I > II). Which one of following is a correct statement ?
(1) I moves faster and has higher Rf value than II
(2) II moves faster and has higher Rf value than I
(3) I moves slower and has higher Rf value than II
(4) II moves slower and has higher Rf value than I
52. Which of the following statements is not true ?
(1) Step growth polymerisation requires a bifunctional monomer.
(2) Nylon 6 is an example of step growth polymerisation.
(3) Chain growth polymerization includes both homopolymerisation and copolymerisation.
(4) Chain growth polymerization involves homopolymerisation only.
53. When 2-butyne is treated with H2/ Lindlar’s catalyst, compound X is produced as the major product and when treated with Na/liq. NH3 it produces Y as the major product. Which of the following statements is correct ?
(1) X will have higher dipole moment and higher boiling point than Y.
(2) Y will have higher dipole moment and higher boiling point than X.
(3) X will have lower dipole moment and lower boiling point than Y.
(4) Y will have higher dipole moment and lower boiling point than X.
54. The increasing order of the acidity of the following carboxylic acids is :
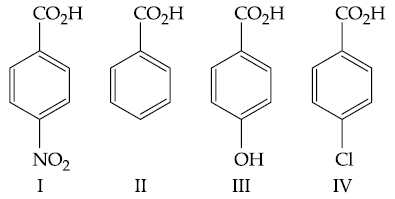
(1) I < III < II < IV
(2) IV < II < III < I
(3) II < IV < III < I
(4) III < II < IV < I
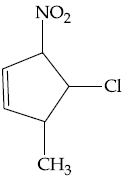
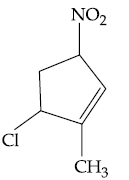
55. The major product formed in the following reaction is :
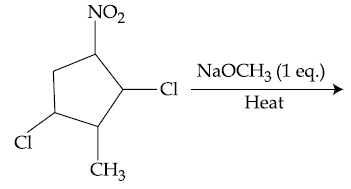
(1) 
(2) 
(3) 
(4) 
56. On treatment of the following compound with a strong acid, the most susceptible site for bond cleavage is :
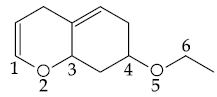
(1) C1 – O2
(2) O2 – C3
(3) C4 – O5
(4) O5 – C6
57. The increasing order of diazotisation of the following compounds is :


(1) (a) < (b) < (c) < (d)
(2) (a) < (d) < (b) < (c)
(3) (a) < (d) < (c) < (b)
(4) (d) < (c) < (b) < (a)
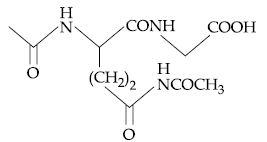
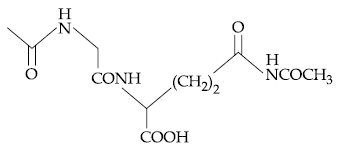
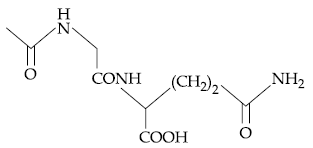
58. The dipeptide, Gln-Gly, on treatment with CH3COCl followed by aqueous work up gives :
(1) 
(2) 
(3) 
(4) 
59. The total number of optically active compounds formed in the following reaction is :

(1) Two
(2) Four
(3) Six
(4) Zero
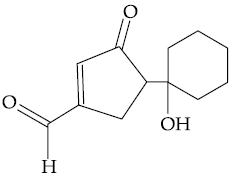
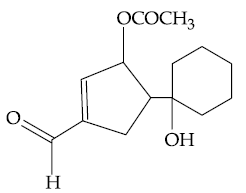
60. The major product formed in the following reaction is :
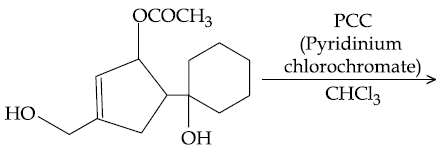
(1) 
(2) 
(3) 
(4) 
61. Let f : A → B be a function defined as ![]() where A = R – {2} and B R – {1}. Then f is :
where A = R – {2} and B R – {1}. Then f is :
(1) invertible and ![]()
(2) invertible and ![]()
(3) invertible and ![]()
(4) not invertible
62. If f (x) is a quadratic expression such that f (1)+f (2)=0, and −1 is a root of f (x)=0, then the other root of f (x)=0 is :
(1) −5/8
(2) −8/5
(3) 5/8
(4) 8/5
63. If |z – 3 + 2i| ≤ 4 then the difference between the greatest value and the least value of |z| is :
(1) 2√13
(2) 8
(3) 4 + √13
(4) √13
64. Suppose A is any 3×3 non-singular matrix and (A − 3I) (A − 5I) = O, where I = I3 and O = O3. If αA + βA−1 = 4I, then α + β is equal to :
(1) 8
(2) 7
(3) 13
(4) 12
65. If the system of linear equations
x + ay + z = 3
x + 2y + 2z = 6
x + 5y + 3z = b
has no solution, then :
(1) a=−1, b=9
(2) a=−1, b ≠ 9
(3) a ≠−1, b=9
(4) a=1, b ≠ 9
66. The number of four letter words that can be formed using the letters of the word BARRACK is :
(1) 120
(2) 144
(3) 264
(4) 270
67. The coefficient of x10 in the expansion of (1+x)2(1+x2)3(1+x3)4 is equal to :
(1) 52
(2) 56
(3) 50
(4) 44
68. If a, b, c are in A.P. and a2, b2, c2 are in G.P. such that a < b < c and ![]() then the value of a is :
then the value of a is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
69. Let  and Bn = 1 – An. Then, the least odd natural number p, so that Bn > An, for all n ≥ p, is :
and Bn = 1 – An. Then, the least odd natural number p, so that Bn > An, for all n ≥ p, is :
(1) 9
(2) 7
(3) 11
(4) 5
70. 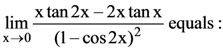
(1) 1/4
(2) 1
(3) 1/2
(4) −1/2
71. Let 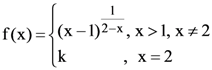
The value of k for which f is continuous at x = 2 is :
(1) 1
(2) e
(3) e−1
(4) e−2
72. If  equals :
equals :
(1) −√3 loge √3
(2) √3 loge √3
(3) −√3 loge 3
(4) √3 loge 3
73. Let f (x) be a polynomial of degree 4 having extreme values at x = 1 and x = 2.
If 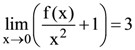 then f(−1) is equal to :
then f(−1) is equal to :
(1) 9/2
(2) 5/2
(3) 3/2
(4) 1/2
74. If 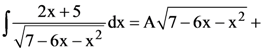
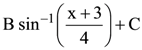
(where C is a constant of integration), then the ordered pair (A, B) is equal to :
(1) (2, 1)
(2) (−2, −1)
(3) (−2, 1)
(4) (2, −1)
75. The value of integral  is :
is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
76. If 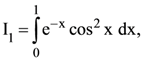
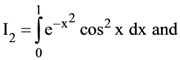
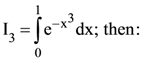
(1) I2 > I3 > I1
(2) I2 > I1 > I3
(3) I3 > I2 > I1
(4) I3 > I1 > I2
77. The curve satisfying the differential equation, (x2 − y2)dx+2xydy=0 and passing through the point (1, 1) is :
(1) a circle of radius one.
(2) a hyperbola.
(3) an ellipse.
(4) a circle of radius two.
78. The sides of a rhombus ABCD are parallel to the lines, x−y+2=0 and 7x−y+3=0. If the diagonals of the rhombus intersect at P(1, 2) and the vertex A (different from the origin) is on the y-axis, then the ordinate of A is :
(1) 5/2
(2) 7/4
(3) 2
(4) 7/2
79. The foot of the perpendicular drawn from the origin, on the line, 3x+y=λ(λ ≠ 0) is P. If the line meets x-axis at A and y-axis at B, then the ratio BP : PA is :
(1) 1 : 3
(2) 3 : 1
(3) 1 : 9
(4) 9 : 1
80. The tangent to the circle C1 : x2+y2 − 2x−1=0 at the point (2, 1) cuts off a chord of length 4 from a circle C2 whose centre is (3, −2). The radius of C2 is :
(1) 2
(2) √2
(3) 3
(4) √6
81. Tangents drawn from the point (−8, 0) to the parabola y2 = 8x touch the parabola at P and Q. If F is the focus of the parabola, then the area of the triangle PFQ (in sq. units) is equal to :
(1) 4x2 + 9y2 = 121
(2) 9x2 + 4y2 = 169
(3) 4x2 – 9y2 = 121
(4) 9x2 – 4y2 = 169
82. A normal to the hyperbola, 4x2 − 9y2 = 36 meets the co-ordinate axes x and y at A and B, respectively. If the parallelogram OABP (O being the origin) is formed, then the locus of P is :
(1) 4x2 + 9y2 = 121
(2) 9x2 + 4y2 = 169
(3) 4x2 – 9y2 = 121
(4) 9x2 – 4y2 = 169
83. An angle between the lines whose direction cosines are given by the equations, l + 3m + 5n = 0 and 5lm −2mn + 6nl = 0, is :
(1) cos−1 (1/3)
(2) cos−1 (1/4)
(3) cos−1 (1/6)
(4) cos−1 (1/8)
84. A plane bisects the line segment joining the points (1, 2, 3) and (−3, 4, 5) at right angles. Then this plane also passes through the point :
(1) (−3, 2, 1)
(2) (3, 2, 1)
(3) (−1, 2, 3)
(4) (1, 2, −3)
85. If the position vectors of the vertices A, B and C of a ∆ABC are respectively ![]() and
and ![]() then the position vector of the point, where the bisector of ∠A meets BC is :
then the position vector of the point, where the bisector of ∠A meets BC is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
86. A player X has a biased coin whose probability of showing heads is p and a player Y has a fair coin. They start playing a game with their own coins and play alternately. The player who throws a head first is a winner. If X starts the game, and the probability of winning the game by both the players is equal, then the value of ‘p’ is :
(1) 1/5
(2) 1/3
(3) 2/5
(4) 1/4
87. If the mean of the data : 7, 8, 9, 7, 8, 7, λ, 8 is 8, then the variance of this data is :
(1) 7/8
(2) 1
(3) 9/8
(4) 2
88. The number of solutions of sin 3x=cos 2x, in the interval (π/2, π) is :
(1) 1
(2) 2
(3) 3
(4) 4
89. A tower T1 of height 60 m is located exactly opposite to a tower T2 of height 80 m on a straight road. From the top of T1, if the angle of depression of the foot of T2 is twice the angle of elevation of the top of T2, then the width (in m) of the road between the feet of the towers T1 and T2 is :
(1) 10√2
(2) 10√3
(3) 20√3
(4) 20√2
90. Consider the following two statements :
Statement p :
The value of sin 120° can be derived by taking θ = 240° in the equation ![]()
Statement q :
The angles A, B, C and D of any quadrilateral ABCD satisfy the equation ![]()
Then the truth values of p and q are respectively :
(1) F, T
(2) T, F
(3) T, T
(4) F, F
Latest Govt Job & Exam Updates: