JEE Main Online Computer Based Test (CBT) Examination Morning Held on 16-04-2018
Timing : 9 : 30 AM – 12 : 30 PM
1. The percentage errors in quantities P, Q, R and S are 0.5%, 1%, 3% and 1.5% respectively in the measurement of a physical quantity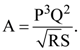 
The maximum percentage error in the value of A will be :
(1) 6.0%
(2) 7.5%
(3) 8.5%
(4) 6.5%
2. Let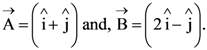 
The magnitude of a coplanar vector 
such that 
is given by :
(1) 
(2) 
(3) 
(4) 
3. A body of mass m starts moving from rest along x-axis so that its velocity varies as 
where a is a constant and s is the distance covered by the body. The total work done by all the forces acting on the body in the first t seconds after the start of the motion is :
(1) 
(2) 8 m a4t2
(3) 4 m a4t2
(4) 
4. Two particles of the same mass m are moving in circular orbits because of force, given by
The first particle is at a distance r=1, and the second, at r=4. The best estimate for the ratio of kinetic energies of the first and the second particle is closest to :
(1) 6 × 10−2
(2) 3 × 10−3
(3) 10−1
(4) 6 × 102
5. An oscillator of mass M is at rest in its equilibrium position in a potential 
A particle of mass m comes from right with speed u and collides completely inelastically with M and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after 13 collisions is : (M = 10, m = 5, u = 1, k = 1)
(1) 
(2) 1/2
(3) 2/3
(4) 
6. Suppose that the angular velocity of rotation of earth is increased. Then, as a consequence :
(1) Weight of the object, everywhere on the earth, will increase.
(2) Weight of the object, everywhere on the earth, will decrease.
(3) There will be no change in weight anywhere on the earth.
(4) Except at poles, weight of the object on the earth will decrease.
7. A thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and zʹ axes will be :
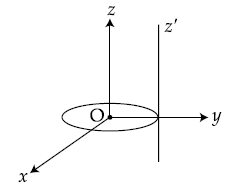
(1) 1 : 3
(2) 1 : 4
(3) 1 : 5
(4) 1 : 2
8. The relative uncertainty in the period of a satellite orbiting around the earth is 10−2. If the relative uncertainty in the radius of the orbit is negligible, the relative uncertainty in the mass of the earth is :
(1) 10−2
(2) 2 × 10−2
(3) 3 × 10−2
(4) 6 × 10−2
9. A small soap bubble of radius 4 cm is trapped inside another bubble of radius 6 cm without any contact. Let P2 be the pressure inside the inner bubble and P0, the pressure outside the outer bubble. Radius of another bubble with pressure difference P2 − P0 between its inside and outside would be :
(1) 12 cm
(2) 2.4 cm
(3) 6 cm
(4) 4.8 cm
10. One mole of an ideal monoatomic gas is taken along the path ABCA as shown in the PV diagram. The maximum temperature attained by the gas along the path BC is given by :
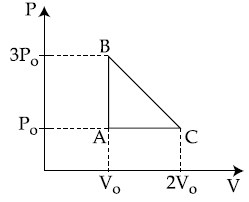
(1) 
(2) 
(3) 
(4) 
11. Two moles of helium are mixed with n moles of hydrogen. If 
for the mixture, then the value of n is :
(1) 1
(2) 3
(3) 2
(4) 3/2
12. A particle executes simple harmonic motion and is located at x=a, b and c at times to, 2to and 3to The frequency of the oscillation is :
(1) 
(2) 
(3) 
(4) 
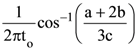
13. Two sitar strings, A and B, playing the note ‘Dha’ are slightly out of tune and produce beats of frequency 5 Hz. The tension of the string B is slightly increased and the beat frequency is found to decrease by 3 Hz. If the frequency of A is 425 Hz, the original frequency of B is :
(1) 430 Hz
(2) 420 Hz
(3) 428 Hz
(4) 422 Hz
14. Two identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameters, and the force between them is F. A third identical conducting sphere, C, is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to :
(1) F
(2) 3F/4
(3) 3F/8
(4) F/2
15. A heating element has a resistance of 100 Ω at room temperature. When it is connected to a supply of 220 V, a steady current of 2 A passes in it and temperature is 500°C more than room temperature. What is the temperature coefficient of resistance of the heating element ?
(1) 0.5 × 10−4 °C−1
(2) 5 × 10−4 °C−1
(3) 1 × 10−4 °C−1
(4) 2 × 10−4 °C−1
16. A galvanometer with its coil resistance 25 Ω requires a current of 1 mA for its full deflection. In order to construct an ammeter to read up to a current of 2 A, the approximate value of the shunt resistance should be :
(1) 2.5 × 10−3 Ω
(2) 1.25 × 10−2 Ω
(3) 1.25 × 10−3 Ω
(4) 2.5 × 10−2 Ω
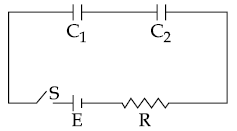
17. In the following circuit, the switch S is closed at t=0. The charge on the capacitor C1 as a function of time will be given by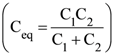 
(1) C1E [1 − exp(−tR/C1)]
(2) C2E [1 − exp(−t/RC2)]
(3) CeqE [1 − exp(−t/RCeq)]
(4) CeqE exp (−t/RCeq)
18. A coil of cross-sectional area A having n turns is placed in a uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
(1) 3 nBAω
(2) 
(3) nBAω
(4) 
19. A charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity ω with respect to normal axis then the magnetic moment of the loop is :
(1) q ωr2
(2) 
(3) 
(4) 
20. A power transmission line feeds input power at 2300 V to a step down transformer with its primary windings having 4000 turns, giving the output power at 230 V. If the current in the primary of the transformer is 5 A, and its efficiency is 90%, the output current would be :
(1) 50 A
(2) 45 A
(3) 25 A
(4) 20 A
21. A plane electromagnetic wave of wavelength λ has an intensity I. It is propagating along the positive Y-direction. The allowed expressions for the electric and magnetic fields are given by :
(1) 
(2) 
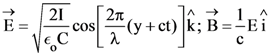
(3) 
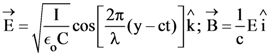
(4) 
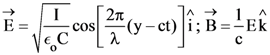
22. A ray of light is incident at an angle of 60° on one face of a prism of angle 30°. The emergent ray of light makes an angle of 30° with incident ray. The angle made by the emergent ray with second face of prism will be :
(1) 0°
(2) 90°
(3) 45°
(4) 30°
23. Unpolarized light of intensity I is incident on a system of two polarizers, A followed by B. The intensity of emergent light is I/2. If a third polarizer C is placed between A and B, the intensity of emergent light is reduced to I/3. The angle between the polarizers A and C is θ. Then :
(1) 
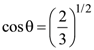
(2) 
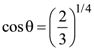
(3) 
(4) 
24. The de-Broglie wavelength (λB) associated with the electron orbiting in the second excited state of hydrogen atom is related to that in the ground state (λG) by :
(1) λB = 2λG
(2) λB = 3λG
(3) λB = λG/2
(4) λB = λG/3
25. Both the nucleus and the atom of some element are in their respective first excited states. They get de-excited by emitting photons of wavelengths λN, λA The ratio 
is closest to :
(1) 10−6
(2) 10
(3) 10−10
(4) 10−1
26. At some instant, a radioactive sample S1 having an activity 5 μCi has twice the number of nuclei as another sample S2 which has an activity of 10 μCi. The half lives of S1 and S2 are :
(1) 20 years and 5 years, respectively
(2) 20 years and 10 years, respectively
(3) 5 years and 20 years, respectively
(4) 10 years and 20 years, respectively
27. In the given circuit, the current through zener diode is :
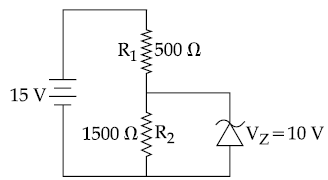
(1) 5.5 mA
(2) 6.7 mA
(3) 2.5 mA
(4) 3.3 mA
28. A carrier wave of peak voltage 14 V is used for transmitting a message signal. The peak voltage of modulating signal given to achieve a modulation index of 80% will be :
(1) 7 V
(2) 28 V
(3) 11.2 V
(4) 22.4 V
29. In a circuit for finding the resistance of a galvanometer by half deflection method, a 6 V battery and a high resistance of 11 kΩ are used. The figure of merit of the galvanometer is 60 μA/division. In the absence of shunt resistance, the galvanometer produces a deflection of θ = 9 divisions when current flows in the circuit. The value of the shunt resistance that can cause the deflection of θ/2, is closest to :
(1) 550 Ω
(2) 220Ω
(3) 55Ω
(4) 110Ω
30. The end correction of a resonance column is 1 cm. If the shortest length resonating with the tuning fork is 10 cm, the next resonating length should be :
(1) 28 cm
(2) 32 cm
(3) 36 cm
(4) 40 cm
31. An unknown chlorohydrocarbon has 3.55% of chlorine. If each molecule of the hydrocarbon has one chlorine atom only; chlorine atoms present in 1 g of chlorohydrocarbon are :
(Atomic wt. of Cl=35.5 u; Avogadro constant=6.023 × 1023 mol−1)
(1) 6.023 × 1020
(2) 6.023 × 109
(3) 6.023 × 1021
(4) 6.023 × 1023
32. The gas phase reaction 2NO2(g) → N2O4(g) is an exothermic reaction. The decomposition of N2O4, in equilibrium mixture of NO2(g) and N2O4(g), can be increased by :
(1) lowering the temperature.
(2) increasing the pressure.
(3) addition of an inert gas at constant volume.
(4) addition of an inert gas at constant pressure.
33. Assuming ideal gas behaviour, the ratio of density of ammonia to that of hydrogen chloride at same temperature and pressure is : (Atomic wt. of Cl=35.5 u)
(1) 1.46
(2) 0.46
(3) 1.64
(4) 0.64
34. When 9.65 ampere current was passed for 1.0 hour into nitrobenzene in acidic medium, the amount of p-aminophenol produced is :
(1) 9.81 g
(2) 10.9 g
(3) 98.1 g
(4) 109.0 g
35. For which of the following processes, ΔS is negative ?
(1) H2(g) → 2H(g)
(2) N2(g, 1 atm) → N2(g, 5 atm)
(3) C(diamond) → C(graphite)
(4) N2(g, 273 K) → N2(g, 300 K)
36. Which one of the following is not a property of physical adsorption ?
(1) Higher the pressure, more the adsorption
(2) Lower the temperature, more the adsorption
(3) Greater the surface area, more the adsorption
(4) Unilayer adsorption occurs
37. If 50% of a reaction occurs in 100 second and 75% of the reaction occurs in 200 second, the order of this reaction is :
(1) Zero
(2) 1
(3) 2
(4) 3
38. Which of the following statements is false ?
(1) Photon has momentum as well as wavelength.
(2) Splitting of spectral lines in electrical field is called Stark effect.
(3) Rydberg constant has unit of energy.
(4) Frequency of emitted radiation from a black body goes from a lower wavelength to higher wavelength as the temperature increases.
39. At 320 K, a gas A2 is 20% dissociated to A(g). The standard free energy change at 320 K and 1 atm in J mol−1 is approximately : (R=8.314 JK−1 mol−1; ln 2=0.693; ln 3=1.098)
(1) 4763
(2) 2068
(3) 1844
(4) 4281
40. The mass of a non-volatile, non-electrolyte solute (molar mass=50 g mol−1) needed to be dissolved in 114 g octane to reduce its vapour pressure to 75%, is :
(1) 37.5 g
(2) 75 g
(3) 150 g
(4) 50 g
41. The incorrect statement is :
(1) Cu2+ salts give red coloured borax bead test in reducing flame.
(2) Cu2+ and Ni2+ ions give black precipitate with H2S in presence of HCl solution.
(3) Ferricion gives blood red colour with potassium thiocyanate.
(4) Cu2+ ion gives chocolage coloured precipitate with potassium ferrocyanide solution.
42. The incorrect geometry is represented by :
(1) BF3 – trigonal planar
(2) H2O – bent
(3) NF3 – trigonal planar
(4) AsF5 – trigonal bipyramidal
43. In Wilkinson’s catalyst, the hybridization of central metal ion and its shape are respectively :
(1) sp3d, trigonal bipyramidal
(2) sp3, tetrahedral
(3) dsp2, square planar
(4) d2sp3, octahedral
44. Among the oxides of nitrogen : N2O3, N2O4 and N2O5 ; the molecule(s) having nitrogen-nitrogen bond is/are :
(1) Only N2O5
(2) N2O3 and N2O5
(3) N2O4 and N2O5
(4) N2O3 and N2O4
45. Which of the following complexes will show geometrical isomerism ?
(1) aquachlorobis(ethylenediamine) cobalt(II) chloride
(2) pentaaquachlorochromium(III) chloride
(3) potassium amminetrichloroplatinate (II)
(4) potassium tris(oxalato)chromate(III)
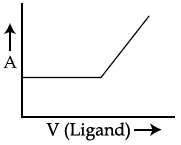
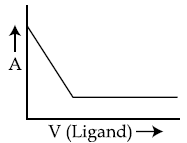
46. In a complexometric titration of metal ion with ligand M(Metal ion)+L(Ligand) → C(Complex) end point is estimated spectrophotometrically (through light absorption). If ‘M’ and ‘C’ do not absorb light and only ‘L’ absorbs, then the titration plot between absorbed light (A) versus volume of ligand ‘L’ (V) would look like :
(1) 
(2) 
(3) 
(4) 
47. In the extraction of copper from its sulphide ore, metal is finally obtained by the oxidation of cuprous sulphide with :
(1) Fe2O3
(2) Cu2O
(3) SO2
(4) CO
48. Which of the following conversions involves change in both shape and hybridisation ?
(1) NH3 → NH4+
(2) CH4 → C2H6
(3) H2O → H3O+
(4) BF3 → BF4−
49. A group 13 element ‘X’ reacts with chlorine gas to produce a compound XCl3 . XCl3 is electron deficient and easily reacts with NH3 to form Cl3X ← NH3 adduct; however, XCl3 does not dimerize. X is :
(1) B
(2) Al
(3) Ga
(4) In
50. When XO2 is fused with an alkali metal hydroxide in presence of an oxidizing agent such as KNO3 ; a dark green product is formed which disproportionates in acidic solution to afford a dark purple solution. X is :
(1) Ti
(2) V
(3) Cr
(4) Mn
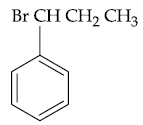
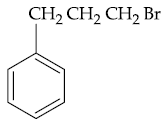
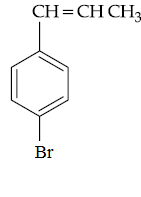
51. The major product of the following reaction is :
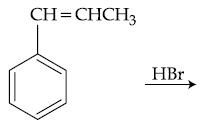
(1) 
(2) 
(3) 
(4) 
52. For standardizing NaOH solution, which of the following is used as a primary standard ?
(1) Ferrous Ammonium Sulfate
(2) dil. HCl
(3) Oxalic acid
(4) Sodium tetraborate
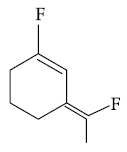
53. The most polar compound among the following is :
(1) 
(2) 
(3) 
(4) 
54. The correct match between items of List – I and List – II is :
(1) (A)-(R), (B)-(S), (C)-(P), (D)-(Q)
(2) (A)-(S), (B)-(R), (C)-(P), (D)-(Q)
(3) (A)-(S), (B)-(R), (C)-(Q), (D)-(P)
(4) (A)-(R), (B)-(S), (C)-(Q), (D)-(P)
55. Among the following, the incorrect statement is :
(1) Maltose and lactose has 1, 4-glycosidic linkage.
(2) Sucrose and amylose has 1, 2-glycosidic linkage.
(3) Cellulose and amylose has 1, 4-glycosidic linkage.
(4) Lactose contains β-D-galactose and β-D-glucose.
56. Which of the following compounds will most readily be dehydrated to give alkene under acidic condition ?
(1) 1-Pentanol
(2) 4-Hydroxypentan-2-one
(3) 3-Hydroxypentan-2-one
(4) 2-Hydroxycyclopentanone
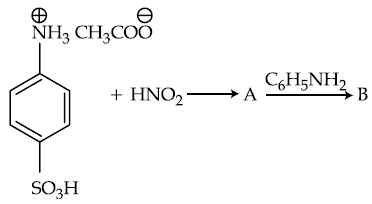
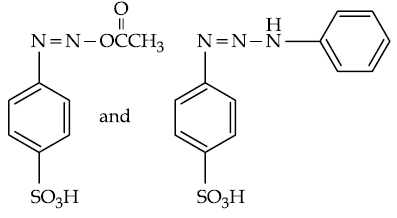
57. Products A and B formed in the following reactions are respectively :
(1) 
(2) 
(3) 
(4) 
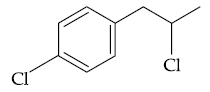
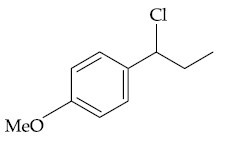
58. The major product B formed in the following reaction sequence is :
(1) 
(2) 
(3) 
(4) 
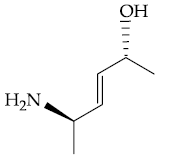
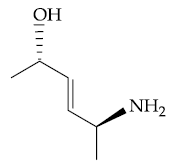
59. The major product of the following reaction is :
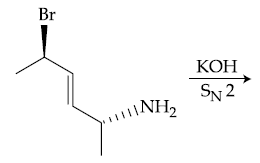
(1) 
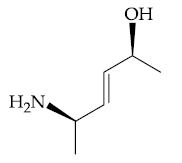
(2) 
(3) 
(4) 
60. The major product of the following reaction is :
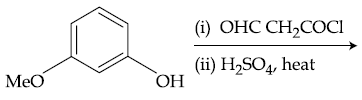
(1) 
(2) 
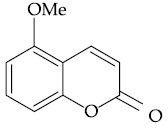
(3) 
(4) 
61. Let N denote the set of all natural numbers. Define two binary relations on N as R1={(x, y) ϵ N × N : 2x + y = 10} and R2={(x, y) ϵ N × N : x + 2y = 10}. Then :
(1) Range of R1 is {2, 4, 8}.
(2) Range of R2 is {1, 2, 3, 4}.
(3) Both R1 and R2 are symmetric relations.
(4) Both R1 and R2 are transitive relations.
62. Let p, q and r be real numbers (p ≠ q, r ≠ 0), such that the roots of the equation 
are equal in magnitude but opposite in sign, then the sum of squares of these roots is equal to :
(1) 
(2) p2 + q2
(3) 2(p2 + q2)
(4) p2 + q2 + r2
63. The least positive integer n for which 
is
(1) 2
(2) 3
(3) 5
(4) 6
64. Let 
and B = A20. Then the sum of the elements of the first column of B is :
(1) 210
(2) 211
(3) 231
(4) 251
65. The number of values of k for which the system of linear equations,
(k + 2)x + 10y = k
kx + (k + 3)y = k – 1
has no solution, is :
(1) 1
(2) 2
(3) 3
(4) infinitely many
66. The number of numbers between 2,000 and 5,000 that can be formed with the digits 0, 1, 2, 3, 4 (repetition of digits is not allowed) and are multiple of 3 is :
(1) 24
(2) 30
(3) 36
(4) 48
67. The coefficient of x2 in the expansion of the product (2− x2) ⋅ ((1 + 2x + 3x2)6+ (1 − 4x2)6) is :
(1) 107
(2) 106
(3) 108
(4) 155
68. Let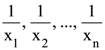 
(xi ≠ 2 for i = 1, 2, . . . , n) be in A.P. such that x1 = 4 and x21 = 20. If n is the least positive integer for which xn > 50, then 
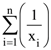is equal to :
(1) 1/8
(2) 3
(3) 13/8
(4) 13/4
69. The sum of the first 20 terms of the series 
is :
(1) 
(2) 
(3) 
(4) 
70. 
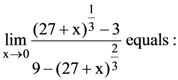
(1) 1/3
(2) −1/3
(3) −1/6
(4) 1/6
71. If the function f defined as 
is continuous at x = 0, then the ordered pair (k, f(0)) is equal to :
(1) (3, 2)
(2) (3, 1)
(3) (2, 1)
(4) (1/3, 2)
72. If 
then 
is equal to :
(1) y/x
(2) x/y
(3) −y/x
(4) −x/y
73. Let M and m be respectively the absolute maximum and the absolute minimum values of the function, f (x)=2x3 − 9x2 + 12x + 5 in the interval [0, 3]. Then M−m is equal to :
(1) 5
(2) 9
(3) 4
(4) 1
74. If 
(C is a constant of integration), then the ordered pair (K, A) is equal to :
(1) (2, 1)
(2) (−2, 3)
(3) (2, 3)
(4) (−2, 1)
75. If 
then :
(1) fʹʹʹ(x) + fʹʹ(x) = sin x
(2) fʹʹʹ(x) + fʹʹ(x) – fʹ(x) = cos x
(3) fʹʹʹ(x) + fʹ(x) = cos x – 2x sin x
(4) fʹʹʹ(x) – fʹʹ(x) = cos x – 2x sin x
76. If the area of the region bounded by the curves, y = x2, y = 1/x and the lines y = 0 and x = t (t > 1) is 1 sq. unit, then it is equal to :
(1) e3/2
(2) 4/3
(3) 3/2
(4) e2/3
77. The differential equation representing the family of ellipses having foci either on the x-axis or on the y-axis, centre at the origin and passing through the point (0, 3) is :
(1) xy yʹʹ + x(yʹ)2 – y yʹ = 0
(2) x + y yʹʹ = 0
(3) xy yʹ + y2 – 9 = 0
(4) xy yʹ – y2 + 9 = 0
78. The locus of the point of intersection of the lines, 
and 
(k is any non-zero real parameter), is :
(1) an ellipse whose eccentricity is 1/√3.
(2) an ellipse with length of its major axis 8√2.
(3) a hyperbola whose eccentricity is √3.
(4) a hyperbola with length of its transverse axis 8√2.
79. If a circle C, whose radius is 3, touches externally the circle, x2 + y2 + 2x − 4y – 4 = 0 at the point (2, 2), then the length of the intercept cut by this circle C, on the x-axis is equal to :
(1) 2√5
(2) 3√2
(3) √5
(4) 2√3
80. Let P be a point on the parabola, x2 = 4y. If the distance of P from the centre of the circle, x2 + y2 + 6x + 8 = 0 is minimum, then the equation of the tangent to the parabola at P, is :
(1) x + 4y – 2 = 0
(2) x – y + 3 = 0
(3) x + y + 1 = 0
(4) x + 2y = 0
81. If the length of the latus rectum of an ellipse is 4 units and the distance between a focus and its nearest vertex on the major axis is 3/2 units, then its eccentricity is :
(1) 1/2
(2) 1/3
(3) 2/3
(4) 1/9
82. The sum of the intercepts on the coordinate axes of the plane passing through the point (−2, −2, 2) and containing the line joining the points (1, −1, 2) and (1, 1, 1), is :
(1) 4
(2) −4
(3) −8
(4) 12
83. If the angle between the lines, 
is then p is 
equal to :
(1) 7/2
(2) 2/7
(3) −7/4
(4) −4/7
84. Let 
and a vector 
be such that 
Then 
equals :
(1) 11/3
(2) 11/√3
(3) 
(4) 
85. The mean and the standard deviation(s.d.) of five observations are 9 and 0, respectively. If one of the observations is changed such that the mean of the new set of five observations becomes 10, then their s.d. is :
(1) 0
(2) 1
(3) 2
(4) 4
86. Let A, B and C be three events, which are pair-wise independent and 
denotes the complement of an event E. If P(A ∩ B ∩ C) = 0 and P(C) > 0, then 
is equal to :
(1) 
(2) 
(3) 
(4) 
87. Two different families A and B are blessed with equal number of children. There are 3 tickets to be distributed amongst the children of these families so that no child gets more than one ticket. If the probability that all the tickets go to the children of the family B is 1/12, then the number of children in each family is :
(1) 3
(2) 4
(3) 5
(4) 6
88. If an angle A of a ΔABC satisfies 5 cosA+3=0, then the roots of the quadratic equation, 9x2 + 27x + 20=0 are :
(1) sec A, cot A
(2) sin A, sec A
(3) sec A, tan A
(4) tan A, cos A
89. A man on the top of a vertical tower observes a car moving at a uniform speed towards the tower on a horizontal road. If it takes 18 min. for the angle of depression of the car to change from 30° to 45° ; then after this, the time taken (in min.) by the car to reach the foot of the tower, is :
(1) 
(2) 
(3) 
(4) 
90. If p→(∼p∨∼q) is false, then the truth values of p and q are respectively :
(1) F, F
(2) T, F
(3) F, T
(4) T, T
Latest Govt Job & Exam Updates: