Physics
Section-A
1. If λ1 and λ2 are the wavelengths of the third member of Lyman and the first member of the Paschen series respectively, then the value of λ1 : λ2 is:
(a) 1 : 3
(b) 1 : 9
(c) 7 : 135
(d) 7 : 108
2. The temperature θ at the junction of two insulating sheets, having thermal resistances R1 and R2 as well as the bottom and top temperatures θ1 and θ2 (as shown in the figure) is given by:
(a) 
(b) 
(c)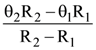 
(d)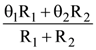 
3. In Young’s double-slit experiment two slits are separated by 2 mm and the screen is placed one meter away. When light of wavelength 500 nm is used, the fringe separation will be:
(a) 0.75 mm
(b) 0.50 mm
(c) 1 mm
(d) 0.25 mm
4. Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: An electron microscope can achieve better resolving power than an optical microscope.
Reason R: The de Broglie’s wavelength of the electrons emitted from an electron gun is much less than the wavelength of visible light.
In light of the above statements, choose the correct answer from the options given below:
(a) A is true but R is false.
(b) Both A and R are true but R is NOT the correct explanation of A.
(c) Both A and R are true and R is the correct explanation of A.
(d) A is false but R is true.
5. Four identical solid spheres each of mass ‘m’ and radius ‘a’ are placed with their centres on the four corners of a square of side ‘b’. The moment of inertia of the system about one side of square where the axis of rotation is parallel to the plane of the square is:
(a) 
(b) 
(c) 
(d) 
6. The normal density of a material is ρ and its bulk modulus of elasticity is K. The magnitude of increase in density of material when a pressure P is applied uniformly on all sides, will be:
(a) ρK/P
(b) K/ρP
(c) PK/ρ
(d) ρP/K
7. LED is constructed from Ga-As-P semiconducting material. The energy gap of this LED is 1.9 eV. Calculate the wavelength of light emitted and its colour.
[h = 6.63 × 10–34 Js and c = 3 × 108 ms–1]
(a) 654 nm and red colour
(b) 1046 nm and blue colour
(c) 1046 nm and red colour
(d) 654 nm and orange colour
8. Five equal resistances are connected in a network as shown in the figure. The net resistance between points A and B is:
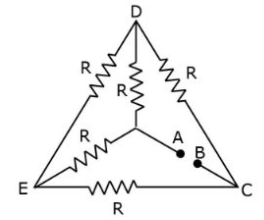
(a) 3R/2
(b) R/2
(c) R
(d) 2R
9. Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If √8R is the distance between the centres of a ring (of mass ‘m’) and a sphere (of mass ‘M’) where both have equal radius ‘R’.
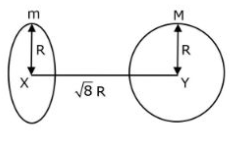
(a) 
(b) 
(c) 
(d) 
10. Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth’s centre, where ‘R’ is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period:
(a) 
(b) 
(c) 
(d) 
11. Find the electric field E at point P (as shown in the figure) on the perpendicular bisector of a uniformly charged thin wire of length L carrying a charge Q. The distance of the point P from the centre of the rod is 
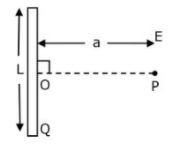
(a) 
(b)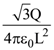 
(c)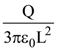 
(d)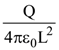 
12. Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: Body ‘P’ having mass M moving with speed ‘u’ has head-on collision elastically with another body ‘Q’ having mass ‘m’ initially at rest. If m<<M, body ‘Q’ will have a maximum speed equal to ‘2u’ after collision.
Reason R: During elastic collision, the momentum and kinetic energy are both conserved.
In the light of the above statements, choose the most appropriate answer from the options given below:
(a) A is correct but R is not correct.
(b) Both A and R are correct but R is NOT the correct explanation of A.
(c) A is not correct but R is correct.
(d) Both A and R are correct and R is the correct explanation of A.
13. A short straight object of height 100 cm lies before the central axis of a spherical mirror whose focal length has absolute value |f| = 40 cm. The image of the object produced by the mirror is of height 25 cm and has the same orientation as the object. One may conclude from the information:
(a) Image is real, same side of concave mirror.
(b) Image is virtual, opposite side of convex mirror.
(c) Image is virtual, opposite side of concave mirror.
(d) Image is real, same side of convex mirror.
14. A particle is moving with uniform speed along the circumference of a circle of radius R under the action of a central fictitious force F which is inversely proportional to R3. Its time period of revolution will be given by:
(a) T ∝ R5/2
(b) T ∝ R2
(c) T ∝R4/3
(d) T ∝ R3/2
15. A large number of water drops, each of radius r, combine to have a drop of radius R. If the surface tension is T and mechanical equivalent of heat is J, the rise in heat energy per unit volume will be:
(a) 2T/rJ
(b) 3T/rJ
(c) 
(d) 
16. A planet revolving in elliptical orbit has:
(A) a constant velocity of revolution.
(B) has the least velocity when it is nearest to the sun.
(C) its areal velocity is directly proportional to its velocity.
(D) areal velocity is inversely proportional to its velocity.
(E) to follow a trajectory such that the areal velocity is constant.
Choose the correct answer from the options given below:
(a) A only
(b) E only
(c) D only
(d) C only
17. An alternating current is given by the equation i = i1 sinωt + i2 cosωt. The rms current will be:
(a) 
(b) 
(c)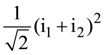 
(d)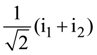 
18. Consider the combination of 2 capacitors C1 and C2, with C2 > C1, when connected in parallel, the equivalent capacitance is 15/4 times the equivalent capacitance of the same connected in series. Calculate the ratio of capacitors, C2/C1.
(a) 15/11
(b) 29/15
(c) 15/4
(d) 111/80
19. If two similar springs each of spring constant K1 are joined in series, the new spring constant and time period would be changed by a factor:
(a) 1/2, √2
(b) 1/4, 2√2
(c) 1/2, 2√2
(d) 1/4, √2
20. In a typical combustion engine the work done by a gas molecule is given by 
where x is the displacement, k is the Boltzmann constant and T is the temperature. If α and β are constants, dimensions of α will be:
(a) [M0 L T0]
(b) [M2 L T–2]
(c) [M L T–2]
(d) [M L T–1]
Section-B
21. The mass per unit length of a uniform wire is 0.135 g/cm. A transverse wave of the form y = –0.21sin(x + 30t) is produced in it, where x is in meter and t is in second. Then, the expected value of tension in the wire is x × 10–2 Value of x is __________. (Round-off to the nearest integer)
22. A radiation is emitted by a 1000 W bulb, and it generates an electric field and magnetic field at P, placed at a distance of 2 m. The efficiency of the bulb is 1.25%. The value of the peak electric field at P is x × 10–1 V/m. Value of x is __________. (Rounded-off to the nearest integer)
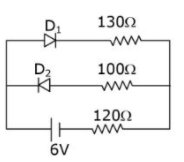
23. The circuit contains two diodes each with a forward resistance of 50 Ω and with infinite reverse resistance. If the battery voltage is 6 V, the current through the 120 Ω resistance is _________ mA.
24. As shown in the figure, a block of mass √3 kg is kept on a horizontal rough surface of coefficient of friction 1/3√3. The critical force to be applied on the vertical surface as shown at an angle 600 with horizontal such that it does not move will be 3x. The value of x will be _______ (upto two decimal places).
[g = 10 m/s2;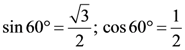 
]
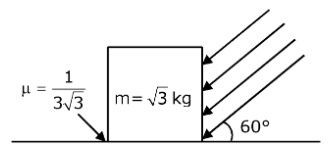
25. In a series LCR resonant circuit, the quality factor is measured as 100. If the inductance is increased by two fold and resistance is decreased by two fold, then the quality factor after this change will be __________. (up to two decimal places).
26. In an electrical circuit, a battery is connected to pass 20 C of charge through it in a certain given time. The potential difference between two plates of the battery is maintained at 15 V. The work done by the battery is __________ J.
27. A container is divided into two chambers by a partition. The volume of the first chamber is 4.5 litre and the second chamber is 5.5 litre. The first chamber contains 3.0 mole of gas at pressure 2.0 atm and the second chamber contain 4.0 mole of identical gas at pressure 3.0 atm. After the partition is removed and the mixture attains equilibrium, then, the common equilibrium pressure existing in the mixture is x × 10–1 Value of x is _______.
28. A boy pushes a box of mass 2 kg with a force 
on a frictionless surface. If the box was initially at rest, then __________m is displacement along the x-axis after 10 s.
29. The maximum and minimum amplitude of an amplitude-modulated wave is 16 V and 8 V respectively. The modulation index for this amplitude modulated wave is x × 10–2. The value of x is ________.
30. A person standing on a spring balance inside a stationary lift measures 60 kg. The weight of that person if the lift descends with uniform downward acceleration of 1.8 m/s2 will be ___________ N. [g =10m/s2]
Chemistry
Section-A
1. B reacts with Hydroxyl amine but does not give Tollens test. Identify A and B.
(a) 1,1-Dichlorobutane and 2-Butanone
(b) 2,2- Dichlorobutane and Butan-2-one
(c) 2,2- Dichlorobutane and Butanal
(d) 1,1- Dichlorobutane and Butanal
2. Match List-I with List-II.
List –I List-II
(Ore) (Element Present)
(a) Kernite (i) Tin
(b) Cassiterite (ii) Boron
(c) Calamine (iii) Fluorine
(d) Cryolite (iv) Zinc
(a) (a) – (ii), (b) – (iv), (c) – (i), (d) – (iii)
(b) (a) – (ii), (b) – (i), (c) – (iv), (d) – (iii)
(c) (a) – (i), (b) – (iii), (c) – (iv), (d) – (ii)
(d) (a) – (iii), (b) – (i), (c) – (ii), (d) – (iv)
3. For the given reaction:
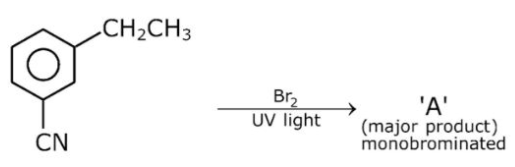
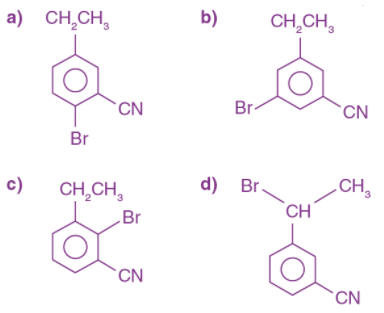
4. The orbital having two radial as well as two angular nodes is
(a) 5d
(b) 4f
(c) 3p
(d) 4d
5. Given below are two statement:
Statement I: o-Nitrophenol is steam volatile due to intramolecular hydrogen bonding
Statement II: o-Nitrophenol has high melting point due to hydrogen bonding.
(a) Both Statement I and Statement II are false
(b) Statement I is false but Statement II is true
(c) Both Statement I and Statement II are true
(d) Statement I is true but Statement II is false
6. An amine on reaction with benzenesulfonyl chloride produces a compound insoluble in alkaline solution. This amine can be prepared by ammonolysis of ethyl chloride. The correct structure of amine is:
(a) CH3CH2NH−CH2CH3
(b) CH3CH2CH2NHCH3
(c) 
(d) CH3CH2NH2
7. For the given reaction: What is A?
8. Statement about heavy water are given below
(A) Heavy water is used in exchange reactions for the study of reaction mechanisms
(B) Heavy water is prepared by exhaustive electrolysis of water
(C) Heavy water has higher boiling point than ordinary water
(D) Viscosity of H2O is greater than D2O
(a) A and B only
(b) A, B and C only
(c) A and D only
(d) A and C only
9. Which of the following is ‘a’ FALSE statement?
(a) Carius tube used in the estimation of sulphur in an organic compound (i) and (iv) are isotopes
(b) Kjeldahl’s method is used for the estimation of nitrogen in an organic compound (ii) and (iii) are isotopes
(c) Phosphoric acid produced on oxidation of phosphorus present in an organic compound is precipitated as Mg2P2O7 by adding magnesia mixture
(d) Carius method is used for the estimation of nitrogen in an organic compound
10. Given below are two statements:
Statement I: A mixture of chloroform and aniline can be separated by simple distillation
Statement II: When separating aniline from a mixture of aniline and water by steam distillation aniline boils below its boiling point
In the light of the above statements, choose the most appropriate answer from the options given below:
(a) Statement I is true, statement II is false
(b) Both Statement I and Statement II are true
(c) Both Statement I and Statement II are false
(d) Statement I is false, Statement II is true
11. Which of the following vitamin is helpful in delaying the blood clotting?
(a) Vitamin B
(b) Vitamin C
(c) Vitamin K
(d) Vitamin E
12. The presence of ozone in troposphere:
(a) Generates photochemical smog
(b) Protects us from the UV radiation
(c) Protects us from the X-ray radiation
(d) Protects us from greenhouse effect
13. On treating a compound with warm dil. H2SO4, gas X is evolved which turns K2Cr2O7 paper acidified with dil. H2SO4 to a green compound Y. X and Y respectively are:
(a) X = SO2, Y = Cr2 (SO4)3
(b) X = SO2, Y = Cr2O3
(c) X = SO3, Y = Cr2O3
(d) X = SO3, Y = Cr2 (SO4)3
14. Find A, B and C in the following reaction:
NH3 + A + CO2 → (NH4)2CO3
(NH4)2CO3 + H2O + B → NH4HCO3
NH4HCO3 + NaCl → NH4Cl + C
(a) A – H2O; B – CO2; C – NaHCO3
(b) A – H2O; B – O2; C – Na2CO3
(c) A – O2; B – CO2; C – Na2CO3
(d) A – H2O; B – O2; C – NaHCO3
15. Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: Dipole-dipole interactions are the only non-covalent interactions, resulting in hydrogen bond formation
Reason R: Fluorine is the most electronegative element and hydrogen bonds in HF are symmetrical
In the light of the above statements, choose the most appropriate answer from the options given below:
(a) A is false but R is true
(b) Both A and R are true and R is the correct explanation of A
(c) A is true but R is false
(d) Both A and R are true and R is not the correct explanation of A
16. Match List-I with List-II.
List-I List-II
Electronic configuration of elements ∆iH in kJ mol−1
(a) 1s22s2 (i) 801
(b) 1s22s22p4 (ii) 899
(c) 1s22s22p3 (iii) 1314
(d) 1s22s22p1 (iv) 1402
(a) (a) – (ii), (b) – (iii), (c) – (iv), (d) – (i)
(b) (a) – (iv), (b) – (i), (c) – (ii), (d) – (iii)
(c) (a) – (i), (b) – (iv), (c) – (iii), (d) – (ii)
(d) (a) – (i), (b) – (iii), (c) – (iv), (d) – (ii)
17. Which one of the following lanthanoids does not form MO2?
[M is lanthanoid metal]
(a) Nd
(b) Yb
(c) Dy
(d) Pr
18. Identify the major products A and B respectively in the following reaction of phenol:
19. The structure of Neoprene is:
20. Compound A used as a strong oxidizing agent is amphoteric in nature. It is the part of lead storage batteries. Compound A is:
(a) Pb3O4
(b) PbO2
(c) PbSO4
(d) PbO
Section-B
21. 224 mL of SO2(g) at 298 K and 1 atm is passed through 100 mL of 0.1 M NaOH solution. The non-volatile solute produced is dissolved in 36 g of water. The lowering of vapour pressure of solution (assuming the solution is dilute) (P(H2O)= 24 mm of Hg) is 10–2 x mm of Hg, the value of x is _____
22. Consider the following reaction
MnO4− + 8H+ + 5e− → Mn+2 + 4H2O, E° = 1.51 V.
The quantity of electricity required in Faraday to reduce five moles of MnO4− is_______.
23. 12 g of oxygen is adsorbed on 1.2 g of platinum metal. The value of oxygen adsorbed per gram of the adsorbent at 1 atm and 300 K in L is _______.
[R = 0.0821 L atm K–1 mol–1]
24. The number of significant figures in 50000.020 × 10–3 is _______.
25. Number of bridging CO ligands in [Mn2(CO)10] is _____.
26. For a chemical reaction A +B ⇌ C + D (ΔrHψ = 80 kJ mol–1) the entropy change ΔrSψ depends on the temperature T (in K) as ΔrSψ = 2T (J K–1 mol–1). Minimum temperature at which it will become spontaneous is ________K.
27. An exothermic reaction X → Y has an activation energy 30 kJ mol–1. If energy change ΔE during the reaction is –20 kJ, then the activation energy for the reverse reaction in kJ is ______.
28. A certain gas obeys P(Vm – b) = RT. The value of 
The value of x is ______.
29. A homogeneous ideal gaseous reaction AB2(g) ⇌ A(g) + 2B(g) is carried out in a 25 liter flask at 27° The initial amount of AB2 was 1 mole and the equilibrium pressure was 1.9 atm. The value of Kp is x × 10–2. The value of x is ______. [R = 0.08206 dm3 atm K–1 mol–1]
30. Dichromate ion is treated with base, the oxidation number of Cr in the product formed is:
Mathematics
Section-A
1. The number of seven-digit integers with the sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only is:
(a) 77
(b) 42
(c) 35
(d) 82
2. The maximum value of the term independent of ‘t’ in the expansion of 
where x ∈ (0, 1) is :
(a)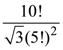 
(b)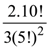 
(c) 
(d) 
3. The value of 
where [x] is the greatest integer ≤ x, is :
(a) 10(e – 1)
(b) 100e
(c) 100(1 – e)
(d) 100(1 + e)
4. The rate of growth of bacteria in a culture is proportional to the number of bacteria present and the bacteria count is 1000 at initial time t = 0. The number of bacteria has increased by 20% in 2 hours. If the population of bacteria is 2000 after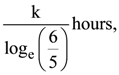 
then 
is equal to :
(a) 4
(b) 2
(c) 16
(d) 8
5. If 
are perpendicular, then 
is equal to:
(a)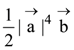 
(b) 
(c) 
(d) 
6. In an increasing geometric series, the sum of the second and the sixth term is 25/2 and the product of the third and fifth term is 25. Then, the sum of 4th, 6th and 8th terms is equal to :
(a) 35
(b) 30
(c) 26
(d) 32
7. Consider the three planes
P1 : 3x + 15y + 21z = 9,
P2 : x – 3y – z = 5, and
P3 : 2x + 10 y + 14z = 5
Then, which one of the following is true ?
(a) P1 and P3 are parallel.
(b) P2 and P3 are parallel.
(c) P1 and P2 are parallel.
(d) P1, P2 and P3 all are parallel.
8. The sum of the infinite series 
is equal to :
(a) 9/4
(b) 15/4
(c) 13/4
(d) 11/4
9. The value of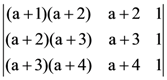 
is:
(a) −2
(b) (a + 1) (a + 2) (a + 3)
(c) 0
(d) (a + 2) (a + 3) (a + 4)
10. If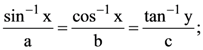 
0 < x < 1, then the value of 
is :
(a) 
(b) 
(c) 1 – y2
(d) 
11. Let A be a symmetric matrix of order 2 with integer entries. If the sum of the diagonal elements of A2 is 1, then the possible number of such matrices is :
(a) 6
(b) 1
(c) 4
(d) 12
12. The intersection of three lines x – y = 0 and x + 2y = 3 and 2x + y = 6 is a:
(a) Equilateral triangle
(b) Right angled triangle
(c) Isosceles triangle
(d) None of the above
13. The maximum slope of the curve 
occurs at the point:
(a) (2, 9)
(b) (2, 2)
(c) (3, 21/2)
(d) (0, 0)
14. Let f be any function defined on R and let it satisfy the condition:
|f (x) − f (y)| ≤ |(x − y)2|, ∀ x, y ∈ R. If f (0) = 1, then :
(a) f(x) < 0, ∀ x ∈ R
(b) f(x) can take any value in R
(c) f(x) = 0, ∀ x ∈ R
(d) f(x) > 0, ∀ x ∈ R
15. The value of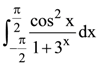 
is:
(a) 2π
(b) 4π
(c) π/2
(d) π/4
16. The value of 
is:
(a) 3/4
(b) 2/√3
(c) 4/3
(d) 2/3
17. A fair coin is tossed a fixed number of times. If the probability of getting 7 heads is equal to the probability of getting 9 heads, then the probability of getting 2 heads is:
(a) 15/212
(b) 15/213
(c) 15/214
(d) 15/28
18. If (1, 5, 35), (7, 5, 5), (1, λ, 7) and (2 λ, 1, 2) are coplanar, then the sum of all possible values of λ is:
(a) −44/5
(b) 39/5
(c) −39/5
(d) 44/5
19. Let R = {P, Q) |P and Q are at the same distance from the origin} be a relation, then the equivalence class of (1, –1) is the set :
(a) S = {(x, y)|x2 + y2 = 1}
(b) S = {(x, y)|x2 + y2 = 4}
(c) S = {(x, y)|x2 + y2 = √2}
(d) S = {(x, y)|x2 + y2 = 2}
20. In the circle given below, let OA = 1 unit, OB = 13 unit and PQ perpendicular to OB. Then, the area of the triangle PQB (in square units) is :
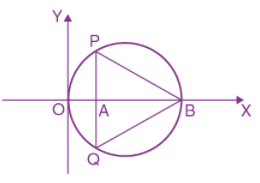
(a) 26√3
(b) 24√2
(c) 24√3
(d) 26√2
Section-B
21. The area bounded by the lines y = |x − 1| − 2 is ______.
22. The number of integral values of ‘k’ for which the equation 3 sin x + 4 cos x = k + 1 has a solution, k ∈ R is ______.
23. Let m, n ∈ N and gcd (2, n) = 1. If 
then n + m is equal to ______.
24. If y = y(x) is the solution of the equation 
y(0) = 0; then 
is equal to ________.
25. The number of solutions of the equation log4 (x − 1) = log2 (x −3) is ______.
26. If √3 (cos2 x) = (√3 − 1) cos x + 1 the number of solutions of the given equation when x ∈ [0, π/2] is _______.
27. Let (λ, 2, 1) be a point on the plane which passes through the point (4, –2, 2). If the plane is perpendicular to the line joining the points (–2, –21, 29) and (–1, –16, 23), then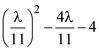 
is equal to______.
28. The difference between degree and order of a differential equation that represents the family of curves given by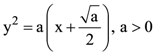 
is _______.
29. The sum of 162th power of the roots of the equation x3 − 2x2 + 2x − 1 = 0 is _________.
30. The value of the integral 
is ______.
Latest Govt Job & Exam Updates: