Physics
Section-A
1. In a series LCR resonance circuit, if we change the resistance only, from a lower to higher value :
(a) The resonance frequency will increase
(b) The quality factor will increase
(c) The quality factor and the resonance frequency will remain constant
(d) The bandwidth of the resonance circuit will increase
2. A radioactive sample disintegrates via two independent decay processes having half-livesT1/21 and T1/22 The effective half-life, T1/2 of the nuclei is:
(a) None of the above
(b) 
(c)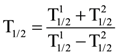 
(d)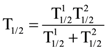 
3. In the experiment of Ohm’s law, a potential difference of 5.0 V is applied across the end of a conductor of length 10.0 cm and diameter of 5.00 mm. The measured current in the conductor is 2.00 A. The maximum permissible percentage error in the resistivity of the conductor is:
(a) 7.5
(b) 3.9
(c) 8.4
(d) 3.0
4. An AC source rated 220V, 50 Hz is connected to a resistor. The time taken by the current to change from its maximum to the rms value is:
(a) 0.25 ms
(b) 25 ms
(c) 2.5 ms
(d) 2.5 s
5. Four identical long solenoids A, B, C and D are connected to each other as shown in the figure. If the magnetic field at the centre of A is 3 T, the field at the centre of C would be: (Assume that the magnetic field is confined within the volume of the respective solenoid.)
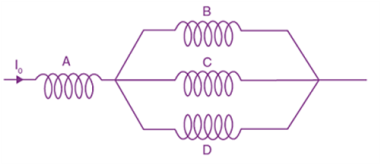
(a) 6T
(b) 12T
(c) 1T
(d) 9T
6. A plane electromagnetic wave of frequency 100 MHz is travelling in a vacuum along the x-direction. At a particular point in space and time, 
(where, 
is unit vector along z-direction). What is 
at this point ? (speed of light c = 3 × 108 m/s)
(a) 
(b) 
(c)
(d) 
7. A particle is travelling, 4 times as fast as an electron. Assuming the ratio of the de-Broglie wavelength of a particle to that of the electron is 2:1, the mass of the particle is :
(a) 1/16 times of mass of e–
(b) 1/6 times the mass of e–
(c) 1/8 times the mass of e–
(d) 8 times the mass of e–
8. What will be the average value of energy along one degree of freedom for an ideal gas in thermal equilibrium at a temperature T? (kB is Boltzmann constant)
(a) kBT
(b) (2/3)kB T
(c) (3/2) kB T
(d) (1/2) kB T
9. Your friend is having an eyesight problem. She is not able to see clearly a distant uniform window mesh and it appears to her as non-uniform and distorted. The doctor diagnosed the problem as:
(a) Myopia and hypermetropia
(b) Astigmatism
(c) Myopia with astigmatism
(d) Presbyopia with astigmatism
10. The time period of a simple pendulum is given by 
The measured value of the length of the pendulum is 10 cm known to a 1 mm accuracy. The time for 200 oscillations of the pendulum is found to be 100 seconds using a clock of 1 s resolution. The percentage accuracy in the determination of ‘g’ using this pendulum is ‘x’. The value of ‘x’ to the nearest integer is.
(a) 5%
(b) 4%
(c) 3%
(d) 2%
11. An oil drop of radius 2 mm with a density of 3 g cm–3 is held stationary under a constant electric field 3.55 × 105 V m–1 in Millikan’s oil drop experiment. What is the number of excess electrons that the oil drop will possess? Consider g = 9.81 m/s2.
(a) 1.73 × 1010
(b) 48.8 × 1011
(c) 1.73 × 1012
(d) 17.3 × 1010
12. The time period of a satellite in a circular orbit of radius R is T. The period of another satellite in a circular orbit of radius 9R is :
(a) 3 T
(b) 9 T
(c) 27 T
(d) 12 T
13. A loop of flexible wire of irregular shape carrying current is placed in an external magnetic field. Identify the effect of the field on the wire
(a) Loop assumes a circular shape with its plane parallel to field
(b) Shape of the loop remains unchanged
(c) Wire gets stretched to become straight
(d) Loop assumes circular shape with its plane normal to the field
14. In Young’s double-slit arrangement, slits are separated by a gap of 0.5 mm, and the screen is placed at a distance of 0.5 m from them. The distance between the first and the third bright fringe formed when the slits are illuminated by monochromatic light of 5890 Å is:
(a) 1178 × 10−6 m
(b) 1178 × 10−9 m
(c) 5890 × 10−7 m
(d) 1178 × 10−12 m
15. Match List – I with List – II
List – I
(a) 10 km height over earth’s surface
(b) 70 km height over earth’s surface
(c) 180 km height over earth’s surface
(d) 270 km height over earth’s surface
List-II
(i) Thermosphere
(ii) Mesosphere
(iii) stratosphere
(iv) Troposphere
(a) (a) – (ii), (b) – (i), (c) – (iv), (d) – (iii)
(b) (a) – (iv), (b) – (iii), (c) – (ii), (d) – (i)
(c) (a) – (iii), (b) – (ii), (c) – (i), (d) – (iv)
(d) (a) – (i), (b) – (iv), (c) – (iii), (d) – (ii)
16. A constant power delivering machine has towed a box, which was initially at rest, along a horizontal straight line. The distance moved by the box in time ‘t’ is proportional to:
(a) t
(b) t3/2
(c) t1/2
(d) t2/3
Answer: (b)
[/bg_collapse]
17. A thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become:
(a) 
(b) 
(c) 
(d) 
18. Imagine that the electron in a hydrogen atom is replaced by a muon (μ). The mass of a muon particle is 207 times that of an electron and the charge is equal to the charge of an electron. The ionization potential of this hydrogen atom will be:
(a) 27.2 eV
(b) 331.2 eV
(c) 13.6 eV
(d) 2815.2 eV
19. The P-V diagram of a diatomic ideal gas system going under cyclic process as shown in the figure. The work done during an adiabatic process CD is (use γ = 1.4):
(a) 200 J
(b) −500 J
(c) −400 J
(d) 400 J
20. The position, velocity and acceleration of a particle moving with constant acceleration can be represented by:
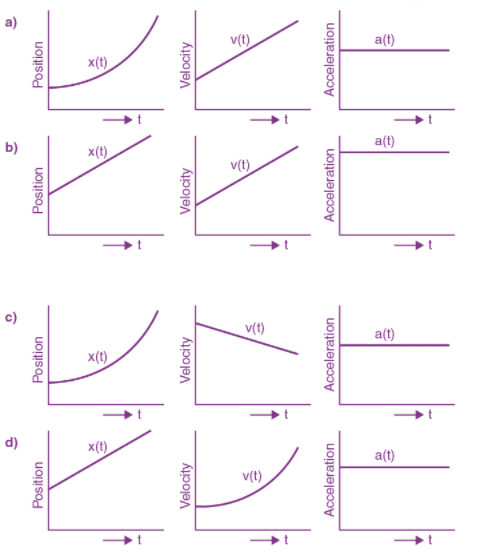
Section-B
21. As shown in the figure, a particle of mass 10 kg is placed at point A. When the particle is slightly displaced to its right, it starts moving and reaches point B. The speed of the particle at B is x m/s. (Take g = 10 m/s2).The value of ‘x’ to the nearest integer is _______.
22. A parallel plate capacitor has a plate area of 100 m2 and plate separation of 10 m. The space between the plates is filled up to a thickness of 5 m with a material of dielectric constant 10. The resultant capacitance of the system is ‘x’ pF. The value of ε0 = 8.85 × 10−12m−1. The value of ‘x’ to the nearest integer is _______.
23. An NPN transistor operates as a common emitter amplifier with a power gain of 106. The input circuit resistance is 100 Ω and the output load resistance is 10 kΩ. The common-emitter current gain ‘β’ will be ______. (Round off to the nearest integer)
24. The voltage across the 10 Ω resistor in the given circuit is x volt.
The value of ‘x’ to the nearest integer is_________.
25. Two separate wires A and B are stretched by 2 mm and 4 mm respectively, when they are subjected to a force of 2 N. Assume that both the wires are made up of the same material and the radius of wire B is 4 times that of the radius of wire A. The length of the wires A and B are in the ratio of a : b, Then a/b can be expressed as 1/x where x is.
26. A bullet of mass 0.1 kg is fired on a wooden block to pierce through it, but it stops after moving a distance of 50 cm into it. If the velocity of the bullet before hitting the wood is 10 m/s and it slows down with uniform deceleration, then the magnitude of effective retarding force on the bullet is ‘x’ N. The value of ‘x’ to the nearest integer is
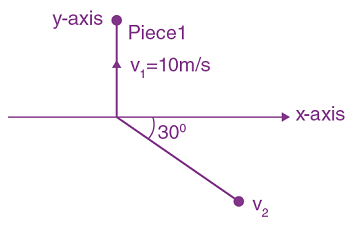
27. A ball of mass 10 kg moving with a velocity 10√ 3 m/s along the x-axis, hits another ball of mass 20 kg which is at rest. After the collision, the first ball comes to rest while the second ball disintegrates into two equal pieces. One-piece starts moving along the y-axis with a speed of 10 m/s. The second piece starts moving at an angle of 30° with respect to the x-axis. The velocity of the ball moving at 30° with x-axis is x m/s. The configuration of pieces after collision is shown in the figure below The value of x to the nearest integer is ______.
28. The circuit shown in the figure consists of a charged capacitor of capacity 3 µF and a charge of 30 µC. At time t = 0, when the key is closed, the value of current flowing through the 5M Ω resistor is ‘x’ µA. The value of ‘x’ to the nearest integer is _______.
29. A person is swimming with a speed of 10 m/s at an angle of 120° with the flow and reaches to a point directly opposite on the other side of the river. Then the speed of the flow is ‘x’ m/s. The value of ‘x’ to the nearest integer is _____.
30. A particle performs simple harmonic motion with a period of 2 second. The time taken by the particle to cover a displacement equal to half of its amplitude from the mean position is 
The value of ‘a’ to the nearest integer is _____.
Chemistry
Section-A
1. The ionic radius of Na+ ion is 1.02 Å. The ionic radii (in Å) of Mg2+ and Al3+, respectively are:
(a) 0.72 and 0.54
(b) 0.68 and 0.72
(c) 1.05 and 0.99
(d) 0.85 and 0.99
2. Match List-I with List-II:
| List-I
(Chemicals) |
List-II
(Use/Preparation/Constituent) |
| (a) Alcoholic potassium hydroxide | (i) electrodes in batteries |
| (b) Pd/BaSO4 | (ii) obtained by addition reaction |
| (c) BHC (Benzene hexachloride | (iii) used for β-elimination reaction |
| (d) Polyacetylene | (iv) Lindlar’s Catalyst |
Choose the most appropriate match:
(a) (a)-(ii), (b)-(i), (c)-(iv), (d)-(iii)
(b) (a)-(iii), (b)-(i), (c)-(iv), (d)-(ii)
(c) (a)-(ii), (b)-(iv), (c)-(i), (d)-(iii)
(d) (a)-(iii), (b)-(iv), (c)-(ii), (d)-(i)
3. The statements that are TRUE:
(A) methane leads to both global warming and photochemical smog
(B) methane is generated from paddy fields
(C) methane is a stronger global warming gas than CO2
(D) methane is a part of reducing smog.
Choose the most appropriate answer from the option given below:
(a) (B), (C), (D) only
(b) (A), (B), (C) only
(c) (A), (B), (D) only
(d) (A) and (B) only
4. Compound with molecular formula C3H6O can show:
(a) Both positional isomerism and metamerism
(b) Metamerism
(c) Positional isomerism
(d) Functional group isomerism
5. Match List-I with List-II:
| List-I | List-II |
| (a) Ca(OCl)2 | (i) Antacid |
| (b) | (ii) Cement |
| (c) CaO | (iii) Bleach |
| (d) CaCO3 | (iv) Plasters of Paris |
Choose the most appropriate answer from the option given below:
(a) (a)-(iii), (b)-(iv), (c)-(ii), (d)-(i)
(b) (a)-(iii), (b)-(ii), (c)-(iv), (d)-(i)
(c) (a)-(iii), (b)-(ii), (c)-(i), (d)-(iv)
(d) (a)-(i), (b)-(iv), (c)-(iii), (d)-(ii)
6. In a binary compound, atoms of element A form a hcp structure and those of element M occupy 2/3 of the tetrahedral voids of the hcp structure. The formula of the binary compound is:
(a) M2A3
(b) MA3
(c) M4A
(d) M4A3
7. Match List-I with List-II:
| List-I
(Class of Drug) |
List-II
(Example) |
| (a) Antacid | (i) Novestrol |
| (b) Artificial Sweetener | (ii) Cimetidine |
| (c) Antifertility | (iii) Valium |
| (d) Tranquilizers | (iv) Alitame |
Choose the most appropriate answer from the option given below:
(a) (a)-(iv), (b)-(iii), (c)-(i), (d)-(ii)
(b) (a)-(ii), (b)-(iv), (c)-(i), (d)-(iii)
(c) (a)-(ii), (b)-(iv), (c)-(iii), (d)-(i)
(d) (a)-(iv), (b)-(i), (c)-(ii), (d)-(iii)
8. Reagent, 1-naphthylamine and sulfanilic acid in acetic acid is used for the detection of:
(a) NO
(b) N2O
(c) NO3−
(d) NO2−
9. The correct structures of trans-[NiBr2(PPh3)2] and meridional-[Co(NH3)3(NO2)3] respectively are:
10. Match List-I with List-II:
List-I List-II
(a) Chlorophyll (i) Ruthenium
(b) Vitamin-B12 (ii) Platinum
(c) Anticancer drug (iii) Cobalt
(d) Grubbs catalyt (iv) Magnesium
Choose the most appropriate answer from the option given below:
(a) (a)-(iv), (b)-(iii), (c)-(i), (d)-(ii)
(b) (a)-(iii), (b)-(ii), (c)-(iv), (d)-(i)
(c) (a)-(iv), (b)-(iii), (c)-(ii), (d)-(i)
(d) (a)-(iv), (b)-(ii), (c)-(iii), (d)-(i)
11. The number of ionisable hydrogens present in the product obtained from a reaction of phosphorus trichloride and phosphonic acid is:
(a) 3
(b) 1
(c) 0
(d) 2
12. A certain orbital has no angular nodes and two radial nodes. The orbital is:
(a) 2p
(b) 3p
(c) 2s
(d) 3s
13. Consider the above chemical reaction and identity product “A”:
14. Given below are two statements: One is labelled as Assertion A and the other is labelled as Reason R:
Assertion A: During the boiling of water having a temporary hardness, Mg(HCO3)2 is converted to MgCO3.
Reason R: The solubility product of Mg(OH)2 is greater than that of MgCO3.
In the light of the above statements, choose the most appropriate answer from the options given below.
(a) A is false but R is true
(b) Both A and R are true and R is the correct explanation of A
(c) Both A and R are true but R is NOT the correct explanation of A
(d) A is true but R is false
15. The chemical is added to reduce the melting point of the reaction mixture during the extraction of aluminium is:
(a) Cryolite
(b) Calamine
(c) Kaolite
(d) Bauxite
16. Considering the below chemical reaction, identity the product “X”:
17. Considering the below reaction, X and Y respectively are:
18. Reaction of Grignard reagent, C2H5MgBr with C8H8O followed by hydrolysis gives compound “A” which reacts instantly with Lucas reagent to give compound B, C10H13 The Compound B is:
19. A non-reducing sugar ”A” hydrolyses to give two reducing monosaccharides. Sugar A is:
(a) Glucose
(b) Fructose
(c) Sucrose
(d) Galactose
20. Match List-I with List-II:
| List-I
(Process) |
List-II
(Catalyst) |
| (a) Deacon’s process | (i) ZSM-5 |
| (b) Contact process | (ii) CuCl2 |
| (c) Cracking of hydrocarbons | (iii) iParticles ’Ni’ |
| (d) Hydrogenation of vegetable oils | (iv) V2O5 |
Choose the most appropriate answer from the option given below:
(a) (a)-(i), (b)-(iii), (c)-(ii), (d)-(iv)
(b) (a)-(iv), (b)-(ii), (c)-(i), (d)-(iii)
(c) (a)-(ii), (b)-(iv), (c)-(i), (d)-(iii)
(d) (a)-(iii), (b)-(i), (c)-(iv), (d)-(ii)
Section-B
21. 2 molal solution of a weak acid HA has a freezing point of 3.885° The degree of dissociation of this acid is _________ × 10–3. (Round off to the Nearest Integer). [Given: Molal depression constant of water = 1.85 K kg mol–1Freezing point of pure water = 0°C]
22. The total number of unpaired electrons present in the complex K3[Cr(oxalate)3] is _______.
23. AX is a covalent diatomic molecule where A and X are second-row elements of the periodic table. Based on Molecular orbital theory, the bond order of AX is 2.5. The total number of electrons in AX is __________. (Round off to the Nearest Integer).
24. ___________ grams of 3-Hydroxy propanal (MW = 74) must be dehydrated to produce 7.8 g of acrolein (MW = 56) (C3H4O) if the percentage yield is 64. (Round off to the Nearest Integer).
[Given: Atomic masses: C : 12.0 u, H : 1.0 u, O : 16.0 u]
25. A reaction of 0.1 mole of Benzyl amine with bromomethane gave 23 g of Benzyl trimethyl ammonium bromide. The number of moles of bromomethane consumed in this reaction are n × 10–1, when n = ___________ . (Round off to the Nearest Integer). [Given: Atomic masses: C: 12.0 u, H : 1.0 u, N : 14.0 u, Br : 80.0 u]
26. 2NO (g) + Cl2 (g) → 2 NOCl (s): This reaction was studied at – 10°C and the following data was obtained.
Run [NO]0 [Cl2]0 r0
1 0.10 0.10 0.18
2 0.10 0.20 0.35
3 0.20 0.20 1.40
[NO]0 and [Cl2]0 are the initial concentrations and r0 is the initial reaction rate. The overall order of the reaction is _________. (Round off to the Nearest Integer).
27. For the reaction: 2Fe3+ (aq) + 2I– (aq) → 2Fe2+ (aq) + I2(s)
The magnitude of the standard molar free energy change, ΔrGm° = – _______ kJ (Round off the Nearest Integer).
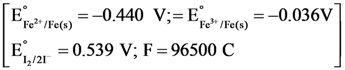
28. For the reaction: C2H6→ C2H4 + H2: The reaction enthalpy ΔrH = __________ kJ mol–1. (Round off to the Nearest Integer).
[Given: Bond enthalpies in kJ mol–1; C – C: 347, C = C : 611; C – H : 414; H – H ; 436]
29. In order to prepare a buffer solution of pH 5.74, sodium acetate is added to acetic acid. If the concentration of acetic acid in the buffer is 1.0 M, the concentration of sodium acetate in the buffer is _________ M. (Round off to the Nearest Integer).
[Given: pKa (acetic acid) = 4.74]
30. Complete combustion of 3 g of ethane gives x × 1022 molecules of water. The value of x is ________. [Round off to the Nearest Integer].
[Use: NA = 6.023 × 1023; Atomic masses in u : C : 12.0; O : 16.0 : H : 1.0 ]
Given: 18
Mathematics
Section-A
1. If the functions are defined as f(x) = √x and 
then what is the common domain of the following functions: f + g, f – g, f / g, g / f, g – f where (f ± g) (x) = f (x) ± g (x), (f / g) (x) =
(a) 0 < x ≤ 1
(b) 0 ≤ x < 1
(c) 0 ≤ x ≤ 1
(d) 0 < x < 1
2. Let α, β, γ be the roots of the equations, x3 + ax2 + bx + c = 0, (a, b, c ∈ R and a, b and a, b ≠ 0). The system of the equations (in u, v, w) given by αu + βv + γw = 0; βu + γv + αw = 0; γu + αv + βw = 0 has non-trivial solutions, then the value of a2/b is
(a) 5
(b) 1
(c) 0
(d) 3
3. If the equation a 
represents a circle where a, d are real constants, then which of the following condition is correct?
(a) |α|2 − ad ≠ 0
(b) |α|2 − ad > 0 and a ∈ R − {0}
(c) α = 0, a, d ∈ R+
(d) |α|2 − ad ≥ 0 and a ∈ R
4. 
is equal to:
(a) 101/404
(b) 101/408
(c) 99/400
(d) 25/101
5. The number of integral values of m so that the abscissa of point of intersection of lines 3x + 4y = 9 and y = mx + 1 is also an integer, is:
(a) 3
(b) 2
(c) 1
(d) 0
6. The solutions of the equation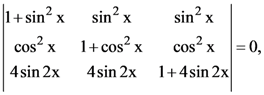 
(0 < x < π), are:
(a) π/6, 5π/6
(b) 7π/12, 11π/12
(c) 5π/12, 7π/12
(d) π/12, π/6
7. If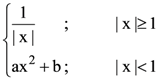 
is differentiable at every point of the domain, then the values of a and b are respectively:
(a) 5/2, −3 / 2
(b) −1/2, 3/2
(c) 1/2, 1/2
(d) 1/2, −3/2
8. A vector a has components 3p and 1 with respect to a rectangular Cartesian system. This system is rotated through a certain angle about the origin in the counterclockwise sense. If with respect to the new system, a has components p + 1 and √10, then a value of p is equal to:
(a) 1
(b) −1
(c) 4/5
(d) −5/4
9. The sum of all the 4-digit distinct numbers that can be formed with the digits 1, 2, 2 and 3 is:
(a) 26664
(b) 122664
(c) 122234
(d) 22264
10. Choose the correct statement about two circles whose equations are given below:
x2 + y2 – 10x – 10y + 41 = 0
x2 + y2 – 22x – 10y + 137 = 0
(a) circles have no meeting point
(b) circles have two meeting points
(c) circles have only one meeting point
(d) circles have the same centre
11. If α, β are natural numbers such that 100α – 199β = (100) (100) + (99) (101) + (98) (102) + …. + (1) (199), then the slope of the line passing through (α, β) and origin is:
(a) 510
(b) 550
(c) 540
(d) 530
12. The value of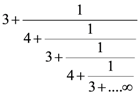 
is equal to:
(a) 3 + 2√3
(b) 4 + √3
(c) 2 + √3
(d) 1.5 + √3
13. The integral 
is equal to:
(where c is a constant of integration)
(a) 
(b) 
(c) 
(d) 
14. The differential equations satisfied by the system of parabolas y2 = 4a (x + a) is:
(a) 
(b)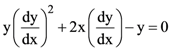 
(c)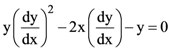 
(d) 
15. The real-valued function 
where [x] denotes the greatest integer less than equal to x, is defined for all x belonging to:
(a) all non- integers except the interval [–1, 1]
(b) all integers except 0, –1, 1
(c) all reals except integers
(d) all reals except the interval [–1, 1]
16. If 
is equal to L, then the value of (6L + 1) is :
(a) 1/2
(b) 2
(c) 1/6
(d) 6
17. For all four circles M, N, O and P, the following four equations are given:
Circle M : x2 + y2 = 1
Circle N : x2 + y2 – 2x = 0
Circle O : x2 + y2 – 2x – 2y + 1 = 0
Circle P : x2 + y2 –2y = 0
If the centre of circle M is joined with the centre of the circle N, further centre of circle N is joined with the centre of the circle O, centre of circle O is joined with the centre of circle P and lastly, the centre of circle P is joined with the centre of circle M, then these lines form the sides of a:
(a) Rectangle
(b) Square
(c) Parallelogram
(d) Rhombus
18. Let (1 + x + 2x2)20 = a0 + a1x + a2x2 + …… + a40x40. Then, a1 + a3 +a5 + ….+ a37 is equal to
(a) 220(220 + 21)
(b) 219(220 + 21)
(c) 220(220 – 21)
(d) 219(220 – 21)
19. Let 
and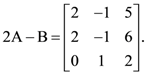 
If Tr(A) denotes the sum of all diagonal elements of the matrix A, then Tr(A) – Tr(B) has value equal to:
(a) 0
(b) 1
(c) 3
(d) 2
20. The equations of one of the straight lines which pass through the point (1, 3) and make an angle tan−1 √2 with the straight line, y + 1 = 3√2x is:
(a) 5√2x + 4y − 15 + 4√2 = 0
(b) 4√2x – 5y − 5 + 4√2 = 0
(c) 4√2x + 5y − 4√2 = 0
(d) 4√2x + 5y − (15 + 4√2) = 0
Section-B
21. The number of times digit 3 will be written when listing the integers from 1 to 1000 is ______.
22. The equation of the planes parallel to the plane x – 2y + 2z – 3 = 0 which are at unit distance from the point (1, 2, 3) is ax + by + cz + d = 0. If (b – d) = K (c – a), then the positive value of K is ______.
23. Let f (x) and g (x) be two functions satisfying f (x2) + g (4 – x) = 4x3 and g (4 –x) + g(x) = 0, then the value of 
is__________.
24. The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If the mean age of the teachers in this school now is 39 years, then the age (in years) of the newly appointed teacher is ______.
25. A square ABCD has all its vertices on the curve x2y2 = 1. The midpoints of its sides also lie on the same curve. Then, the square of the area of ABCD is ______.
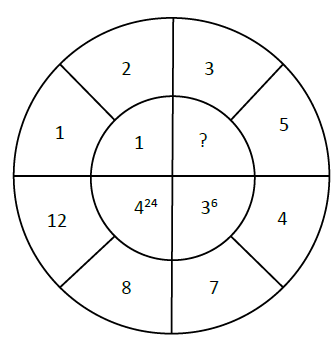
26. The missing value in the following figure is ______.
27. The numbers of solutions of the equation 
in the interval [0, 2π] is _______.
28. Let z1, z2 be the roots of the equations z2 + az + 12 = 0 and z1, z2 form an equilateral triangle with origin. Then, the value of |a| is ______.
29. Let the plane ax + by + cz + d = 0 bisect the line joining the points (4, –3, 1) and (2, 3, –5) at the right angles. If a, b, c, d are integers, then the minimum value of (a2 + b2 + c2 +d2) is ______.
30. If 
f (0) = 0 and 
then the value of K is ________.
Latest Govt Job & Exam Updates: