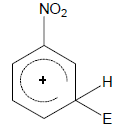
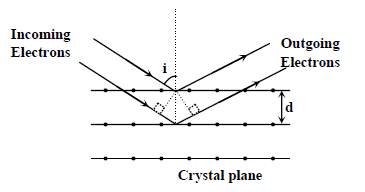
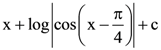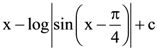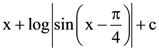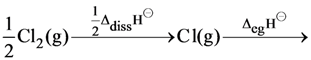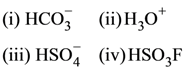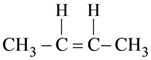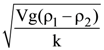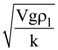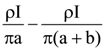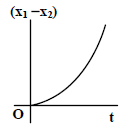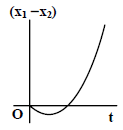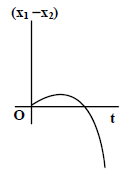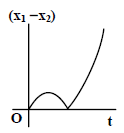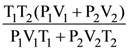JEE MAIN (AIEEE) Past Exam Paper-2009
Physics
Part – A
1. This question contains Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best describes the two statements.
Statement – 1: For a charged particle moving from point P to point Q, the net work done by an electrostatic field on the particle is independent of the path connecting point P to point Q.
Statement-2: The net work done by a conservative force on an object moving along a closed loop is zero
(1) Statement-1 is true, Statement-2 is false
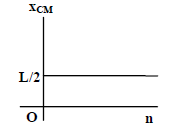
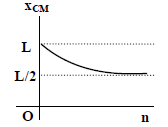
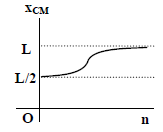
(2) Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation of Statement-1.
(3) Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation of Statement-1.
(4) Statement-1 is false, Statement-2 is true
2. The above is a plot of binding energy per nucleon Eb, against the nuclear mass M; A, B, C, D, E, F correspond to different nuclei. Consider four reactions:
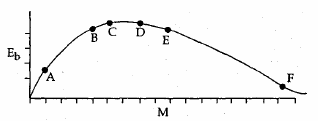
(i) A + B → C + ε (ii) C → A + B + ε
(iii) D + E → F + ε and (iv) F → D + E + ε
where ε is the energy released? In which reactions is ε positive?
(1) (i) and (iv)
(2) (i) and (iii)
(3) (ii) and (iv)
(4) (ii) and (iii)
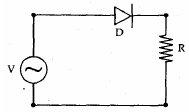
3. A p-n junction (4) shown in the figure can act as a rectifier. An alternating current source (V) is connected in the circuit.
(1) 
(2) 
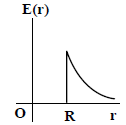
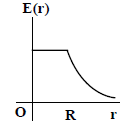
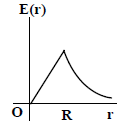
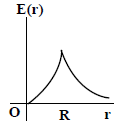
(3) 
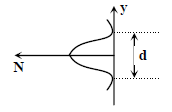
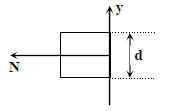
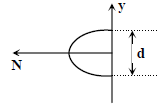
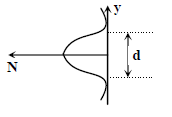
(4) 
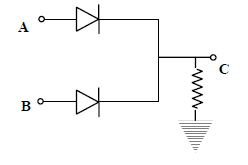
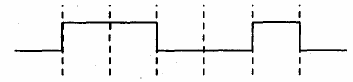
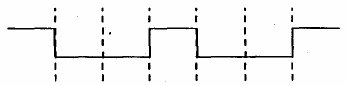
4. The logic circuit shown below has the input waveforms ‘A’ and ‘B’ as shown. Pick out the correct output waveform.
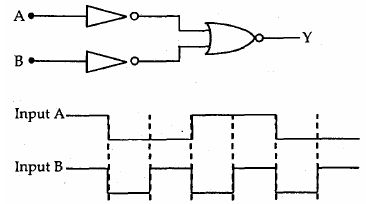
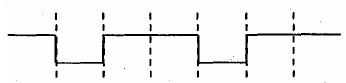
(1) 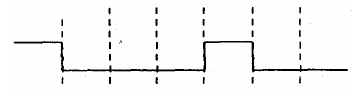
(2) 
(3) 
(4) 
5. If x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
(1) a2T2 + 4π2v2
(2) aT/x
(3) aT + 2πv
(4) aT/v
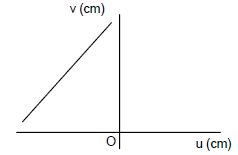
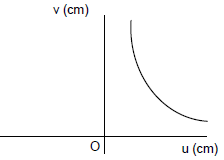
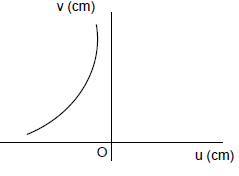
6. In an optics experiment, with the position of the object fixed, a student varies the position of a convex lens and for each position, the screen is adjusted to get a clear image of the object. A graph between the object distance u and the image distance v, from the lens, is plotted using the same scale for the two axes. A straight line passing through the origin and making an angle of 45° with the x-axis meets the experimental curve at P. The coordinates of P will be
(1) (2f, 2f)
(2) (f/2, f/2)
(3) (f, f)
(4) (4f, 4f)
7. A thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of
(1) 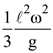
(2) ![]()
(3) 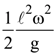
(4) 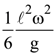
8. Let 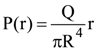 be the charge density distribution for a solid sphere of radius R and total charge Q. for a point ‘p’ inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is
be the charge density distribution for a solid sphere of radius R and total charge Q. for a point ‘p’ inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is
(1) 0
(2) 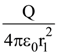
(3) 
(4) 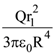
9. The transition from the state n = 4 to n = 3 in a hydrogen like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition from
(1) 2 → 1
(2) 3 → 2
(3) 4 → 2
(4) 5 → 2
10. One kg of a diatomic gas is at a pressure of 8 × 104 N/m2. The density of the gas is 4 kg/m−3. What is the energy of the gas due to its thermal motion?
(1) 3 × 104 J
(2) 5 × 104 J
(3) 6 × 104 J
(4) 7 × 104 J
11. This question contains Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best describes the two statements.
Statement-1: The temperature dependence of resistance is usually given as R = Ro(1 + αΔt). The resistance of a wire changes from 100 Ω to 150 Ω when its temperature is increased from 27°C to 227°C. This implies that α = 2.5 ×10−3 /°C.
Statement 2: R = Ri (1 + αΔT) is valid only when the change in the temperature ΔT is small and ΔR = (R – Ro) << Ro.
(1) Statement-1 is true, Statement-2 is false
(2) Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation of Statement-1.
(3) Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation of Statement-1.
(4) Statement-1 is false, Statement-2 is true
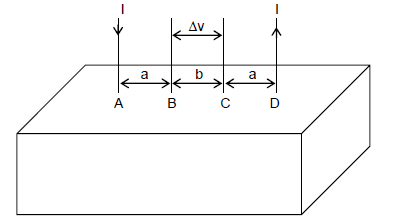
Directions: Question numbers 12 and 13 are based on the following paragraph.
A current loop ABCD is held fixed on the plane of the paper as shown in the figure. The arcs BC (radius = b) and DA (radius = a) of the loop are joined by two straight wires AB and CD. A steady current I is flowing in the loop. Angle made by AB and CD at the origin O is 30°. Another straight thin wire with steady current I1 flowing out of the plane of the paper is kept at the origin.
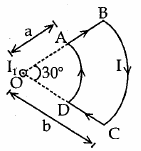
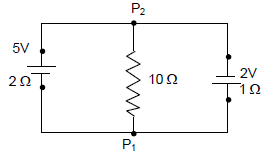
12. The magnitude of the magnetic field (B) due to loop ABCD at the origin (O) is
(1) zero
(2) 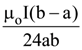
(3) 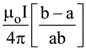
(4) 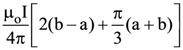
13. Due to the presence of the current I1 at the origin
(1) The forces on AB and DC are zero
(2) The forces on AD and BC are zero
(3) The magnitude of the net force on the loop is given by 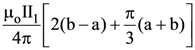
(4) The magnitude of the net force on the loop is given by 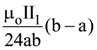
14. A mixture of light, consisting of wavelength 590 nm and an unknown wavelength, illuminates Young’s double slit and gives rise to two overlapping interference patterns on the screen. The central maximum of both lights coincide. Further, it is observed that the third bright fringe of known light coincides with the 4th bright fringe of the unknown light. From this data, the wavelength of the unknown light is
(1) 393.4 nm
(2) 885.0 nm
(3) 442.5 nm
(4) 776.8 nm
15. Two points P and Q are maintained at the potentials of 10V and -4V respectively. The work done in moving 100 electrons from P to Q is
(1) −19 × 10−17 J
(2) 9.60 × 10−17 J
(3) −2.24 × 10−16 J
(4) 2.24 × 10−16 J
16. The surface of a metal is illuminated with the light of 400 nm. The kinetic energy of the ejected photoelectrons was found to be 1.68 eV. The work function of the metal is (hc = 1240 eV nm)
(1) 3.09 eV
(2) 1.41 eV
(3) 151 eV
(4) 1.68 eV
17. A particle has an initial velocity ![]() and an acceleration of
and an acceleration of ![]() Its speed after 10 s is
Its speed after 10 s is
(1) 10 units
(2) 7√2 units
(3) 7 units
(4) 8.5 units
18. A motor cycle starts from rest and accelerates along a straight path at 2 m/s2. At the starting point of the motor cycle there is a stationary electric sire. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was at rest? (speed of sound = 330 ms−1).
(1) 49 m
(2) 98 m
(3) 17 m
(4) 196 m
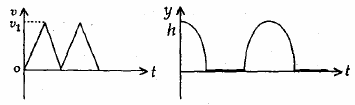
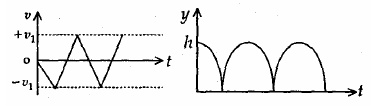
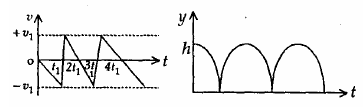
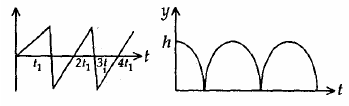
19. Consider a rubber ball freely falling from a height h = 4.9 m onto a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time the height as function of time will be
(1) 
(2) 
(3) 
(4) 
20. A charge Q is placed at each of the opposite corners of a square. A charge q is placed at each of the other two corners. If the net electrical force on Q is zero, then the Q/q equals
(1) −2√2
(2) −1
(3) 1
(4) −1/√2
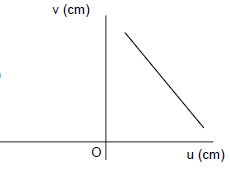
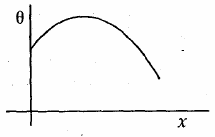
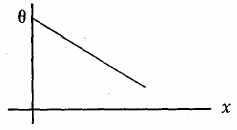
21. A long metallic bar is carrying heat from one of its ends to the other end under steady-state. The variation of temperature θ along the length x of the bar from its hot end is best described by which of the following figure.
(1) 
(2) 
(3) 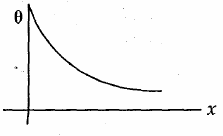
(4) 
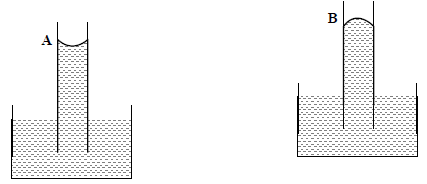
22. A transparent solid cylindrical rod has a refractive index of 2/√ It is surrounded by air. A light ray is incident at the mid point of one end of the rod as shown in the figure.

The incident angle θ for which the light ray grazes along the wall of the rod is
(1) sin−1(1/2)
(2) sin−1(√3/2)
(3) sin−1(2/√3)
(4) sin−1(1/√3)
23. Three sound waves of equal amplitudes have frequencies (v – 1), v, (v + 1). They superpose to give beats. The number of beats produced per second will be
(1) 4
(2) 3
(3) 2
(4) 1
24. The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth is
(1) 2R
(2) R/√2
(3) R/2
(4) √2R
25. Two wires are made of the same material and have the same volume. However wire 1 has crosssectional area A and wire-2 has cross-sectional area 3A. If the length of wire 1 increases by Δx on applying force F, how much force is needed to stretch wire 2 by the same amount?
(1) F
(2) 4F
(3) 6F
(4) 9F
26. In an experiment the angles are required to be measured using an instrument. 29 divisions of the main scale exactly coincide with the 30 divisions of the vernier scale. If the smallest division of the main scale is half-a-degree(=0.5°), then the least count of the instrument is
(1) one minute
(2) half minute
(3) one degree
(4) half degree
27. An inductor of inductance L = 400 mH and resistors of resistances R1 = 2Ω and R2 = 2Ω are connected to a battery of emf 12V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t = 0. The potential drop across L as a function of time is.
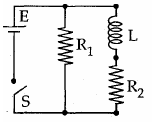
(1) 6e−5tV
(2) ![]()
(3) 6(1 – e−t/0.2)V
(4) 12e−5tV
Directions: Question numbers 28, 29 and 30 are based on the following paragraph. Two moles of helium gas are taken over the cycle ABCDA, as shown in the P – T diagram.
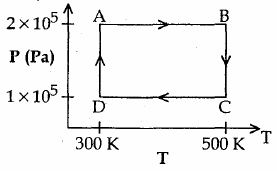
28. Assuming the gas to be ideal the work done on the gas in taking it from A to B is
(1) 200 R
(2) 300 R
(3) 400 R
(4) 500 R
29. The work done on the gas in taking it from D to A is
(1) −414 R
(2) +414 R
(3) −690 R
(4) +690 R
30. The net work done on the gas in the cycle ABCDA is
(1) Zero
(2) 276 R
(3) 1076 R
(4) 1904 R
CHEMISTRY
PART – B
31. Knowing that the Chemistry of lanthanoids (Ln) is dominated by its +3 oxidation state, which of the following statements in incorrect ?
(1) Because of the large size of the Ln (III) ions the bonding in its compounds is predominantly ionic in character.
(2) The ionic sizes of Ln (III) decrease in general with increasing atomic number.
(3) Ln (III) compounds are generally colourless.
(4) Ln (III) hydroxides are mainly basic in character.
32. A liquid was mixed with ethanol and a drop of concentrated H2SO4 was added. A compound with a fruity smell was formed. The liquid was :
(1) CH3OH
(2) HCHO
(3) CH3COCH3
(4) CH3COOH
33. Arrange the carbanions, ![]() in order of their decreasing stability :
in order of their decreasing stability :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
34. The alkene that exhibits geometrical isomerism is :
(1) propene
(2) 2-methyl propene
(3) 2-butene
(4) 2-methyl-2-butene
35. In which of the following arrangements, the sequence is not strictly according to the property written against it ?
(1) CO2 < SiO2 < SnO2 < PbO2 : increasing oxidizing power
(2) HF < HCl < HBr < HI : increasing acid strength
(3) NH3 < PH3 < AsH3 < SbH3 : increasing basic strength
(4) B < C < O < N : increasing first ionization enthalpy.
36. The major product obtained on interaction of phenol with sodium hydroxide and carbon dioxide is :
(1) benzoic acid
(2) salicyladehyde
(3) salicylic acid
(4) phthalic acid
37. Which of the following statements is incorrect regarding physissorptions ?
(1) It occurs because of vander Waal’s forces.
(2) More easily liquefiable gases are adsorbed readily.
(3) Under high pressure it results into multi molecular layer on adsorbent surface.
(4) Enthalpy of adsorption (∆Hadsorption) is low and positive.
38. Which of the following on heating with aqueous KOH, produces acetaldehyde ?
(1) CH3COCl
(2) CH3CH2Cl
(3) CH2ClCH2Cl
(4) CH3CHCl2
39. In an atom, an electron is moving with a speed of 600m/s with an accuracy of 0.005%. Certainity with which the position of the electron can be located is (h = 6.6 × 10−34 kg m2s−1, mass of electron em = 9.1 × 10−31 kg)
(1) 1.52 × 10−4 m
(2) 5.10 × 10−3 m
(3) 1.92 × 10−3 m
(4) 3.84 × 10−3 m
40. In a fuel cell methanol is used as fuel and oxygen gas is used as an oxidizer. The reaction ![]() is At 298 K standard Gibb’s energies of formation for CH3OH(ℓ), H2O(ℓ) and CO2(g) are −2, −237.2 and −394.4 kJ mol−1 respectively. If standard enthalpy of combustion of methanol is −726 kJ mol−1, efficiency of the fuel cell will be
is At 298 K standard Gibb’s energies of formation for CH3OH(ℓ), H2O(ℓ) and CO2(g) are −2, −237.2 and −394.4 kJ mol−1 respectively. If standard enthalpy of combustion of methanol is −726 kJ mol−1, efficiency of the fuel cell will be
(1) 80%
(2) 87%
(3) 90%
(4) 97%
41. Two liquids X and Y form an ideal solution. At 300K, vapour pressure of the solution containing 1 mol of X and 3 mol of Y is 550 mm Hg. At the same temperature, if 1 mol of Y is further added to this solution, vapour pressure of the solution increases by 10 mm Hg. Vapour pressure (in mmHg) of X and Y in their pure states will be, respectively :
(1) 200 and 300
(2) 300 and 400
(3) 400 and 600
(4) 500 and 600
42. The half life period of a first order chemical reaction is 6.93 minutes. The time required for the completion of 99% of the chemical reaction will be (log 2=0.301) :
(1) 230.3 minutes
(2) 23.03 minutes
(3) 46.06 minutes
(4) 460.6 minutes
43. Given : ![]() The value of standard electrode potential for the change,
The value of standard electrode potential for the change, ![]() will be :
will be :
(1) −0.072 V
(2) 0.385 V
(3) 0.770 V
(4) −0.270
44. On the basis of the following thermochemical data : (∆FG°H(aq)+ = 0)
H2O(ℓ) → H+ (aq) + OH−(aq); ∆H = 57.32 kJ
![]()
The value of enthalpy of formation of OH− ion at 25°C is :
(1) −22.88 kJ
(2) −228.88 kJ
(3) +228.88 kJ
(4) −343.52 kJ
45. Copper crystallizes in fcc with a unit cell length of 361 pm. What is the radius of copper atom ?
(1) 108 pm
(2) 127 pm
(3) 157 pm
(4) 181 pm
46. Which of the following has an optical isomer?
(1) [CO(NH3)3Cl]+
(2) [CO(en)(NH3)2]2+
(3) [CO(H2O)4 (en)]3+
(4) [CO(en)2(NH3)2]3+
47. Solid Ba (NO3)2 is gradually dissolved in a 1.0 × 10−4 M Na2CO3 At what concentration of Ba2+ will a precipitate begin to form ? (Ksp for BaCO3 = 5.1 × 10−9).
(1) 4.1 × 10−5 M
(2) 5.1 × 10−5 M
(3) 8.1 × 10−5 M
(4) 8.1 × 10−7 M
48. Which one of t he following reactions of Xenon compounds is not feasible?
(1) XeO3 + 6HF → XeF6 + 3H2O
(2) 3XeF4 + 6H2O → 2Xe + XeO3 + 12HF + 1.5O2
(3) 2XeF4 + 2H2O → 2Xe + 4HF + O2
(4) XeF6 + RbF → Rb(XeF7]
49. Using MO theory predict which of the following species has the shortest bond length ?
(1) O22+
(2) O2+
(3) O2−
(4) O22−
50. In context with the transition elements, which of the following statements is incorrect ?
(1) In addition to the normal oxidation states, the zero oxidation state is also shown by these elements in complexes.
(2) In the highest oxidation states, the transition metal show basic character and form cationic complexes.
(3) In the highest oxidation states of the first five transition elements (Sc to Mn), all the 4s and 3d electrons are used for bonding.
(4) Once the d5 configuration is exceeded, the tendency to involve all the 3d electrons in bonding decreases.
51. Calculate the wavelength (in nanometer) associated with a proton moving at 1.0 ×103 ms−1 (Mass of proton = 1.67 ×10−27 kg and h = 6.63 ×10−34 Js ) :
(1) 0.032 nm
(2) 0.40 nm
(3) 2.5 nm
(4) 14.0 nm
52. A binary liquid solution is prepared by mixing n-heptane and ethanol. Which one of the following statements is correct regarding the behaviour of the solution ?
(1) The solution formed is an ideal solution
(2) The solution is non-ideal, showing +ve deviation from Raoult’s law.
(3) The solution is non-ideal, showing –ve deviation from Raoult’s law.
(4) n-heptane shows +ve deviation while ethanol shows –ve deviation from Raoult’s law.
53. The number of stereoisomers possible for a compound of the molecular formula CH3 − CH = CH − CH OH −Me is :
(1) 3
(2) 2
(3) 4
(4) 6
54. The IUPAC name of neopentane is
(1) 2-methylbutane
(2) 2, 2-dimethylpropane
(3) 2-methylpropane
(4) 2, 2-dimethylbutane
55. The set representing the correct order of ionic radius is :
(1) Li+ > Be2+ > Na+ > Mg2+
(2) Na+ > Li+ > Mg2+ > Be2+
(3) Li+ > Na+ > Mg2+ > Be2+
(4) Mg2+ > Be2+ > Li+ > Na+
56. The two functional groups present in a typical carbohydrate are :
(1) −OH and −COOH
(2) −CHO and −COOH
(3) > C = O and −OH
(4) −OH and −CHO
57. The bond dissociation energy of B – F in BF3 is 646 kJ mol−1 whereas that of C-F in CF4 is 515kJ mol−1 . The correct reason for higher B-F bond dissociation energy as compared to that of C- F is :
(1) smaller size of B-atom as compared to that of C- atom
(2) stronger σ bond between B and F in BF3 as compared to that between C and F in CF4
(3) significant pπ – pπ interaction between B and F in BF3 whereas there is no possibility of such interaction between C and F in CF4.
(4) lower degree of pπ – pπ interaction between B and F in BF3 than that between C and F in CF4.
58. In Cannizzaro reaction given below
![]()
the slowest step is :
(1) the attack of : ![]() at the carboxyl group
at the carboxyl group
(2) the transfer of hybride to the carbonyl group
(3) the abstraction of proton from the carboxylic group
(4) the deprotonation of Ph CH2OH
59. Which of the following pairs represents linkage isomers ?
(1) [Cu(NH3)4] [PtCl4] and [Pt(NH3)4] [CuCl4]
(2) [Pd(P Ph3)2 (NCS)2] and [Pd(P Ph3)2 (SCN)2]
(3) [CO (NH3)5 NO3] SO4 and [CO(NH3)5SO4] NO3
(4) [Pt Cl2(NH3)4]Br2 and [PtBr2(NH3)4]Cl2
60. Buna-N synthetic rubber is a copolymer of :
(1) 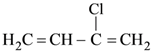 and H2C = CH – CH = CH2
and H2C = CH – CH = CH2
(2) H2C = CH – CH = CH2 and H5C6 – CH = CH2
(3) H2C = CH – CN and H2C = CH – CH = CH2
(4) H2C = CH – CN and 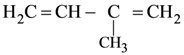
Mathematics
PART – C
61. Let a, b, c be such that b(a + c) ≠ 0 . If 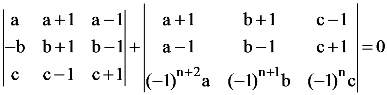 , then the value of ‘n’ is
, then the value of ‘n’ is
(1) zero
(2) any even integer
(3) any odd integer
(4) any integer
62. If the mean deviation of number 1, 1 + d, 1 + 2d, ….. , 1 + 100d from their mean is 255, then the d is equal to
(1) 10.0
(2) 20.0
(3) 10.1
(4) 20.2
63. If the roots of the equation bx2 + cx + a = 0 be imaginary, then for all real values of x, the expression 3b2x2 + 6bcx + 2c2 is
(1) greater than 4ab
(2) less than 4ab
(3) greater than −4ab
(4) less than −4ab
64. Let A and B denote the statements
A: cos α + cos β + cos γ = 0
B: sin α + sin β + sin γ = 0
If cos(β – γ) + cos(γ – α) + cos(α – β) = −3/2, then
(1) A is true and B is false
(2) A is false and B is true
(3) both A and B are true
(4) both A and B are false
65. The lines p(p2 + 1) x – y + q =0 and (p2 + 1)2 x + (p2 + 1)y + 2q = 0 are perpendicular to a common line for
(1) no value of p
(2) exactly one value of p
(3) exactly two values of p
(4) more than two values of p
66. If A, B and C are three sets such that A ∩ B = A ∩ C and A ∪ B = A ∪ C, then
(1) A = B
(2) A = C
(3) B = C
(4) A ∩ B = ϕ
67. If ![]() are non-coplanar vectors and p, q are real numbers, then the equality
are non-coplanar vectors and p, q are real numbers, then the equality ![]() holds for
holds for
(1) exactly one value of (p, q)
(2) exactly two values of (p, q)
(3) more than two but not all values of (p , q)
(4) all values of (p, q)
68. Let the line ![]() lies in the plane x + 3y – αz + β = 0. Then (α, β) equals
lies in the plane x + 3y – αz + β = 0. Then (α, β) equals
(1) (6, −17)
(2) (−6, 7)
(3) (5, −15)
(4) (−5, 15)
69. From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on the shelf so that the dictionary is always in the middle. Then the number of such arrangements is
(1) less than 500
(2) at least 500 but less than 750
(3) at least 750 but less than 1000
(4) at least 1000
70. 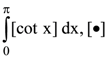 denotes the greatest integer function, is equal to
denotes the greatest integer function, is equal to
(1) π/2
(2) 1
(3) −1
(4) −π/2
71. For real x, let f (x) = x3 + 5x + 1, then
(1) f is one-one but not onto R
(2) f is onto R but not one-one
(3) f is one-one and onto R
(4) f is neither one-one nor onto R
72. In a binomial distribution ![]() if the probability of at least one success is greater than or equal to 9/10, then n is greater than
if the probability of at least one success is greater than or equal to 9/10, then n is greater than
(1) 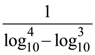
(2) 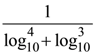
(3) 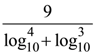
(4) 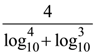
73. If P and Q are the points of intersection of the circles x2 + y2 + 3x + 7y + 2p − 5 = 0 and x2 + y2 + 2x + 2y − p2 = 0 , then there is a circle passing through P, Q and (1, 1) for
(1) all values of p
(2) all except one value of p
(3) all except two values of p
(4) exactly one value of p
74. The projections of a vector on the three coordinate axis are 6, −3, 2 respectively. The direction cosines of the vector are
(1) 6, −3, 2
(2) 6/5, −3/5, 2/5
(3) 6/7, −3/7, 2/7
(4) −6/7, −3/7, 2/7
75. If ![]() then the maximum value of |z| is equal to
then the maximum value of |z| is equal to
(1) √3 + 1
(2) √5 + 1
(3) 2
(4) 2 + √2
76. Three distinct points A, B and C are given in the 2 – dimensional coordinate plane such that the ratio of the distance of any one of them from the point (1, 0) to the distance from the point ( – 1, 0) is equal to 1/3. Then the circumcentre of the triangle ABC is at the point
(1) (0, 0)
(2) (5/4, 0)
(3) (5/2, 0)
(4) (5/3, 0)
77. The remainder left out when 82n – (62)2n + 1 is divided by 9 is
(1) 0
(2) 2
(3) 7
(4) 8
78. The ellipse x2 + 4y2 = 4 is inscribed in a rectangle aligned with the coordinate axes, which in turn in inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is
(1) x2 + 16y2 = 16
(2) x2 + 12y2 = 16
(3) 4x2 + 48y2 = 48
(4) 4x2 + 64y2 = 48
79. The sum to the infinity of the series ![]() is
is
(1) 2
(2) 3
(3) 4
(4) 6
80. The differential equation which represents the family of curves ![]() where c1 and c2 are arbitrary constants is
where c1 and c2 are arbitrary constants is
(1) y’ = y2
(2) y” = y’y
(3) yy” = y’
(4) yy”=(y’)2
81. One ticket is selected at random from 50 tickets numbered 00, 01, 02, …., 49. Then the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals
(1) 1/14
(2) 1/7
(3) 5/14
(4) 1/50
82. Let y be an implicit function of x defined by x2x − 2xx cot y −1= 0 . Then y'(1) equals
(1) −1
(2) 1
(3) log 2
(4) −log 2
83. The area of the region bounded by the parabola (y – 2)2 = x −1, the tangent to the parabola at the point (2, 3) and the x-axis is
(1) 3
(2) 6
(3) 9
(4) 12
84. Given P(x) = x4 + ax3 + bx2 + cx + d such that x = 0 is the only real root of P'(x) = 0 . If P(−1) < P(1) , then in the interval [−1, 1]
(1) P(−1) is the minimum and P(1) is the maximum of P
(2) P(−1) is not minimum but P(1) is the maximum of P
(3) P(−1) is the minimum and P(1) is not the maximum of P
(4) neither P(−1) is the minimum nor P(1) is the maximum of P
85. The shortest distance between the line y − x = 1 and the curve x = y2 is
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
Directions: Question number 86 to 90 are Assertion – Reason type questions. Each of these questions contains two statements
Directions: Question number 86 to 90 are Assertion – Reason type questions. Each of these questions
contains two statements
Statement-1 (Assertion) and Statement-2 (Reason).
Each of these questions also have four alternative choices, only one of which is the correct answer. You have to select the correct choice
86. Let f(x) = (x + 1)2 – 1, x ≥ −1
Statement-1 : The set {x : f(x) = f−1(x)} = {0, −1}
Statement-2 : f is a bijection.
(1) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1
(2) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1
(3) Statement-1 is true, Statement-2 is false
(4) Statement-1 is false, Statement-2 is true
87. Let f (x) = x |x| and g(x) = sinx .
Statement-1 : gof is differentiable at x = 0 and its derivative is continuous at that point.
Statement-2 : gof is twice differentiable at x = 0.
(1) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1
(2) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1
(3) Statement-1 is true, Statement-2 is false
(4) Statement-1 is false, Statement-2 is true
88. Statement-1 : The variance of first n even natural numbers is ![]()
Statement-2 : The sum of first n natural numbers is ![]() and the sum of squares of first n natural numbers is
and the sum of squares of first n natural numbers is ![]()
(1) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1
(2) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1
(3) Statement-1 is true, Statement-2 is false
(4) Statement-1 is false, Statement-2 is true
89. Statement-1 : ~ (p ↔~ q) is equivalent to p ↔ q.
Statement-2 : ~ (p ↔~ q) is a tautology.
(1) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1
(2) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1
(3) Statement-1 is true, Statement-2 is false
(4) Statement-1 is false, Statement-2 is true
90. Let A be a 2 × 2 matrix
Statement-1 : adj(adj A) = A
Statement-2 : |adj A| = |A|
(1) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1
(2) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1
(3) Statement-1 is true, Statement-2 is false
(4) Statement-1 is false, Statement-2 is true
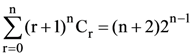
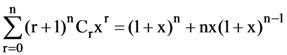
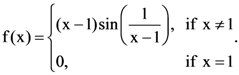 Then which one of the following is true?
Then which one of the following is true?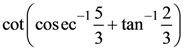 is
is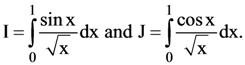 Then which one of the following is true?
Then which one of the following is true?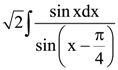 is
is