BITSAT SOLVED PAPER-2019
PART-I : PHYSICS
1. Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
(a)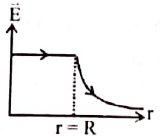 
(b) 
(c)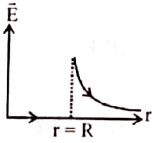 
(d)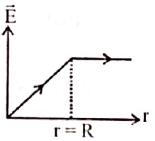 
2. If 
are the electric and magnetic field vectors of e.m. waves then the direction of propagation of e.m. wave is along the direction of
(a) 
(b) 
(c) 
(d) None of these
3. The young’s modulus of a wire of length L and radius r Y N/m2. If the length and radius are reduced to L/2 and r/2, then its young’s modulus will be
(a) Y/2
(b) Y
(c) 2Y
(d) 4Y
4. Twelve resistors each of resistance 16 Ω are connected in the circuit as shown. The net resistance between A and B is
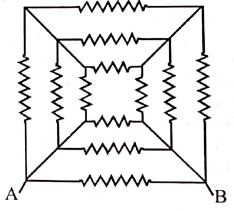
(a) 1 Ω
(b) 2 Ω
(c) 3 Ω
(d) 4 Ω
5. The time period of a satellite of earth is 5 hours. If the separation between the earth and the satellite is increased to 4 times the previous value, the new time period will become
(a) 10 hours
(b) 80 hours
(c) 40 hours
(d) 20 hours
6. Two rains are moving towards each other with speeds of 20 m/s and 15 m/s relative to the ground. The first train sounds a whistle of frequency 600 Hz. The frequency of the whistle heard by a passenger in the second train before the train meets, is (the speed of sound in air is 340 m/s)
(a) 600 Hz
(b) 585 Hz
(c) 645 Hz
(d) 666 Hz
7. You are asked to design a having mirror assuming that a person keeps it 10 cm from his face and views the magnified image of the face at the closest comfortable distance of 25 cm. The radius of curvature of the mirror would then be:
(a) 60 cm
(b) −24 cm
(c) −60 cm
(d) 24 cm
8. A block is kept on a frictionless inclined surface with angle of inclination ‘α’. The incline is given an acceleration ‘a’ to keep the block stationary. Then ‘a’ is equal to
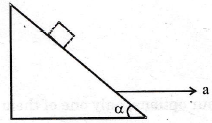
(a) g cosec α
(b) g/tan α
(c) g tan α
(d) g
9. With the increase in temperature, the angle of contact
(a) decreases
(b) increases
(c) remains constant
(d) sometimes increases and sometimes
10. Forward biasing is that in which applied voltage
(a) increases potential barrier
(b) cancels the potential barrier
(c) is equal to 1.5 volt
(d) None of these
11. Number of significant figures in expression 
is
(a) 2
(b) 4
(c) 3
(d) 5
12. The ratio of the specific heats 
in terms of degrees of freedom (n) given by
(a) (1 + n/3)
(b) (1 + 2/n)
(c) (1 + n/2)
(d) (1 + 1/n)
13. A stone is thrown with a velocity u making an angle θ with the horizontal. The horizontal distance covered by its fall to ground is maximum when the angle θ is equal to
(a) 0°
(b) 30°
(c) 45°
(d) 90°
14. A ball of mass 150 g, moving with an acceleration 20 m/s2, is his by a force, which acts on it for 0.1 sec. The impulsive force is
(a) 0.5 N
(b) 0.1 N
(c) 0.3 N
(d) 1.2 N
15. A man drags a block through 10 m on rough surface (μ = 0.5). A force of √3 kN acting at 30° to the horizontal. The work done by applied force is
(a) zero
(b) 7.5 kJ
(c) 5 kJ
(d) 10 kJ
16. A force of 
acts on a body for 4 second, produces a displacement of 
The power used is
(a) 9.5 W
(b) 7.5 W
(c) 6.5 W
(d) 4.5 W
17. The Earth is assumed to be a sphere of radius R. A platform is arranged at a height R from the surface of the Earth. The escape velocity of a body from this platform is fv, where v is its escape velocity from the surface of the Earth. The value of f is
(a) 1/3
(b) 1/2
(c) √2
(d) 1/√2
18. Kepler’s second law regarding constancy of areal velocity of a planet is a consequence of the law of conservation of
(a) Energy
(b) Angular momentum
(c) Linear momentum
(d) None of these
19. Water is flowing through a horizontal tube having cross-sectional areas of its two ends being A and A’ such that ratio A/A’ is 5. If the pressure difference of water between the two ends is 3 × 105 N m−2, the velocity of water with which it enters the tube will be (neglect gravity effects)
(a) 5ms−1
(b) 10 ms−1
(c) 25 ms−1
(d) 50√10 ms−1
20. A thermodynamic system is taken from state A to B along ACB and is brought back to A along BDA as shown in the PV diagram. The net work done during the complete cy cle is given by the area
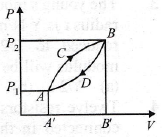
(a) P1ACBP2P1
(b) ACBB’A’A
(c) ACBDA
(d) ADBB’A’A
21. A boat crosses a river from port A to port B, which are just on the opposite side. The speed of the water is Vw and that of boat is VB relative to still water. Assume Vw = 2Vw. What is the time taken by the boat, if it has to cross the river directly on the AB line (D = width of the river]
(a) 
(b) 
(c) 
(d) 
22. Two springs, of force constants k1 and k2 are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
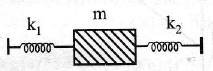
(a) 2f
(b) f/2
(c) f/4
(d) 4f
23. When a potential difference V is applied across a conductor at a temperature T, the drift velocity of electrons is proportional to
(a) √V
(b) V
(c) √T
(d) T
24. The amplitude of a damped oscillator becomes (1/3rd) in 2 seconds. If its amplitude after 6 seconds is 1/n times the original amplitude, the value of n is
(a) 32
(b) 33
(c) ∛3
(d) 23
25. The angular speed of the electron in the nth orbit of Bohr hydrogen atom is
(a) directly proportional to n
(b) inversely proportional to √n
(c) inversely proportional to n2
(d) inversely proportional to n3
26. In the given figure, the charge on 3 μF capacitor is
(a) 10 μC
(b) 15 μC
(c) 30 μC
(d) 5 μC
27. Two bodies A and B are placed in an evacuated vessel maintained at a temperature of 27° The temperature of A is 327°C and that of B is 227°C. The ratio of heat loss from A and B is about
(a) 2 : 1
(b) 1 : 2
(c) 4 : 1
(d) 1 : 4
28. If a rigid body is rotating about an axis with a constant velocity, then
(a) Velocity, Angular velocity of all particles will be same
(b) Velocity, Angular velocity of all particles will be different
(c) Velocity of all particles will be different but angular velocity will be same.
(d) Angular velocity of all particles will be different but velocity will be same.
29. The fundamental frequency of an open organ pipe is 300 Hz. The first overtone of this pipe has same frequency as first overtone of a closed organ pipe. If speed of sound is 330 m/s, then the length of closed organ pipe is
(a) 41 cm
(b) 30 cm
(c) 45 cm
(d) 35 cm
30. In Young’s experiment, the distance between the slits is reduced to half and the distance between the slit and screen is doubled, then the fringe width
(a) will not change
(b) will become half
(c) will be doubled
(d) will become four times
31. If a rolling body’s angular momentum changes by 20 SI units in 3 seconds, by a constant torque. Then find the torque on the b ody
(a) 20/3 SI units
(b) 100/3 SI units
(c) 20 SI units
(d) 5 SI units
32. Charge Q is distributed to two different metallic spheres having radii x and 2x such that both spheres have equal surface charge density, then charge on large sphere is
(a) 4Q/5
(b) Q/5
(c) 3Q/5
(d) 5Q/4
33. In an LR circuit f = 50 Hz, L = 2 H, E = 5 volts, R = 1 Ω then energy stored in inductor is
(a) 50 J
(b) 25 J
(c) 100 J
(d) None of these
34. A straight wire of length 0.5 metre and carrying a current of 1.2 ampere is placed in uniform magnetic field induction 2 tesla. The magnetic field is perpendicular to the length of the wire. The force on the wire is
(a) 2.4 N
(b) 1.2 N
(c) 3.0 N
(d) 2.0 N
35. A man drives a car from station B towards station A at speed 60 km/h. A car leaves station A for station B every 10 min. The distance between A and B is 60 km. The car travels at the speed of 60 km/h. A man drives a car from B towards A at speed of 60 km/h. If he starts at the moment when first car leaves the station B, then how many cars would be meet on the route?
(a) 4
(b) 7
(c) 9
(d) 12
36. In rotatory motion, linear velocities of all the particles of the body are
(a) same
(b) different
(c) zero
(d) cannot say
37. If x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
(a) aT/x
(b) aT + 2πv
(c) aT/v
(d) a2T2 + 4π2v2
38. A conducting wire frame is placed in a magnetic field which is directed into the paper. The magnetic field is increasing at a constant rate. The directions of induced current in wires AB and CD are
(a) B to A and D to C
(b) A to B and C to D
(c) A to B and D to C
(d) B to A and C to D
39. Find the acceleration of block A and B. Assume pulley is massless.
(a) 
(b) 
(c) 
(d) 
40. The nuclei of which one of the following pairs of nuclei are isotones?
(a) 34Se74, 31Ga71
(b) 38Sr84, 38Sr86
(c) 42Mo92, 40Zr92
(d) 20Ca40, 16S32
PART-II : CHEMISTRY
41. Plots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows Arrhenius equation is
(a)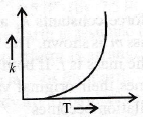 
(b)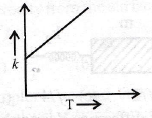 
(c) 
(d)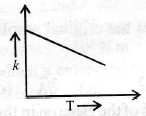 
42. 3.6 g of oxygen is adsorbed on 1.2 g of metal powder. What volume of oxygen adsorbed per gram of the adsorbent at 1 atm and 273 K?
(a) 0.19 L g−1
(b) 1 L g−1
(c) 2.1 L g−1
(d) None of these
43. In the purification of impure nickel by Mond’s process, metal is purified by:
(a) Electrolytic reduction
(b) Vapour phase thermal decomposition
(c) Thermite reduction
(d) Carbon reduction
44. When chlorine water is added to an aqueous solution of sodium iodide in the presence of chloroform, a violet colouration is obtained. ON adding more the chlorine water and vigorous shaking, the violet colour disappears. This shows the conversion of ….. into ….
(a) I2, HIO3
(b) I2, HI
(c) HI, HIO3
(d) I2, HOI
45. In the clathrates of xenon with water, the nature of bonding between xenon and water molecule is
(a) covalent
(b) hydrogen bonding
(c) coordinate
(d) dipole-include dipole
46. The electronic configurations of Eu(Atomic No. 63), Gd(Atomic No. 64) and Tb(Atomic No. 65) are
(a) [Xe]4f76s2, [Xe]4f8 6s2 and [Xe]4f85d16s2
(b) [Xe]4f75d16s2, [Xe]4f7 5d1 6s2 and [Xe]4f96s2
(c) [Xe]4f65d16s2, [Xe]4f75d16s2 and [Xe]4f85d16s2
(d) [Xe]4f76s2, [Xe]4f75d1 6s2 and [Xe]4f96s2
47. Which of the following carbonyls will have the strongest C – O bond?
(a) [Mn(CO)6]+
(b) [Cr(CO)6]
(c) [V(CO6]−
(d) [Fe(CO)5]
48. How many chiral compounds are possible on monochlorination of 2-methyl butane?
(a) 8
(b) 2
(c) 4
(d) 6
49. How many chiral compounds are possible in the reaction of excess of CH3MgBr with C6H5COOC2H5 to make 2-phenyl-2-propanol?
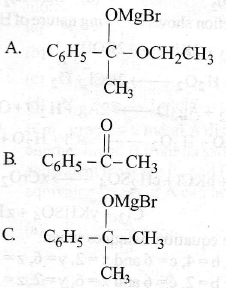
(a) A and B
(b) A, B and C
(c) A and C
(d) B and C
50. 
(a)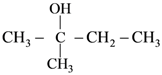 
(b) 
(c)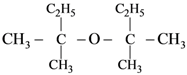 
(d) 
51. Which of the following is the strongest base?
(a) 
(b)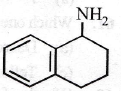 
(c) 
(d) 
52. Which of the following does not reduce Benedict’s solution?
(a) Glucose
(b) Fructose
(c) Sucrose
(d) Aldehyde
53. General formula of solid in zinc blende structure is
(a) AB2
(b) AB3
(c) AB
(d) A2B
54. Glycine in alkaline solution exists as ______ and migrates to
(a) Cation, cathode
(b) Neutral , anode
(c) Zwitter ion, cathode
(d) anion, anode
55. Product on reaction of ethanamide with phosphorus pentoxide is
(a) ethanamine
(b) acetonitrile
(c) ethanol
(d) ethane isonitrile
56. Ka of HX is 10−5, then find concentration of H3O+ when equal volumes of 0.25M HX and 0.05 M NaOH are mixed.
(a) 4 × 10−5 M
(b) 6 × 10−5 M
(c) 8 × 10−3 M
(d) 2 × 10−5 M
57. Net cell reaction of Pt|H2(640 mm)|HCl|H2(510 mm)|Pt.
(a) 0.89V
(b) 0.93V
(c) 2.91 × 10−3 V
(d) 2.5 × 10−2 V
58. Which of the following has zero net dipole moment?
(a) XeF4
(b) BrF3
(c) ClF3
(d) SF4
59. Which of the following element has the highest ionization enthalpy?
(a) Boron
(b) Aluminium
(c) Germanium
(d) Thallium
60. Out of the elements with atomic number 7, 8, 9, 13 which has the smallest size and highest ionization enthalpy?
(a) 7
(b) 8
(c) 9
(d) 13
61. Which one is classified as a condensation polymer?
(a) Dacron
(b) Neoprene
(c) Teflon
(d) Acrylonitrile
62. Which of the following compounds is not an antacid?
(a) Phenelzine
(b) Ranitidie
(c) Aluminium hydroxide
(d) Cimetidine
63. Mole fraction of the solute in a 1.00 molal aqueous solution is
(a) 0.1770
(b) 0.0177
(c) 0.0344
(d) 1.7700
64. The IUPAC name of the following compound is
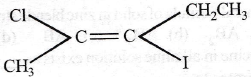
(a) trans-2-chloro-3-iodo-2-pentene
(b) cis-3-iodo-4-chloro-3-penten
(c) trans-3-iodo-4-chloro-3-pentene
(d) cis-2-chloro-3-iodo-2-pentene
65. Most stable carbocation among the following is
(a)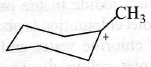 
(b) 
(c)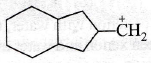 
(d) 
66. Which is correct for the following changes?
(a) X is Lindlar Catalyst, B is cis-2-butene
(b) A is 2-butyne, X is Na-liq. NH3
(c) B is trans-2-butene, X is Na-liq. NH3
(d) A is 2-butene, X is SeO2
67. The stability of +1 oxidation state among Al, Ga, ln and Tl increases in the sequence :
(a) Ga < In < Al < Tl
(b) Al < Ga < ln < Tl
(c) Tl < In < Ga < Al
(d) In < Tl < Ga < Al
68. Which of the following alkaline earth metal hydroxide is amphoteric in character?
(a) Be(OH)2
(b) Ca(OH)2
(c) Sr(OH)2
(d) Ba(OH)2
69. Which reaction show oxidizing nature of H2O2?
(a) H2O2 + 2KI → 2KOH + I2
(b) Cl2 + H2O2 → 2HCl + O2
(c) H2O2 + Ag2O → 2Ag + H2O + O2
(d) NaClO + H2O2 → NaCl + H2O + O2
70. aK2Cr2O7 + bKCl + cH2SO4 → xCrO2Cl2 + yKHSO4 + zH2O
The above equation balances when
(a) a = 2, b = 4, c = 6 and x = 2, y = 6, z = 3
(b) a = 4, b = 2, c = 6 and x = 6, y = 2, z = 3
(c) a = 6, b = 4, c = 2 and x = 6, y = 3, z = 2
(d) a = 1, b = 4, c = 6 and x = 2, y = 6, z = 3
71. For the reactions
A ⇌ B; Kc = 2
B ⇌ C; Kc = 4
C ⇌ D; Kc = 6
Kc for the reaction A ⇌ D is
(a) 2 × 4 × 6
(b) 
(c) 2 + 4 + 6
(d) 
72. Which of the following will always lead to a non-spontaneous change?
(a) ∆H and ∆S both +ve
(b) ∆H is –ve ∆S both +ve
(c) ∆H and ∆S both -ve
(d) ∆H is +ve ∆S both -ve
73. The densities of two gasses are in the ratio of 1 : 16. The ratio of their rates of diffusion is
(a) 16 : 1
(b) 4 : 1
(c) 1 : 4
(d) 1 : 16
74. In the reaction, 2PCl5 ⇌ PCl4+ + PCl6−, the change in hybridization is from
(a) sp3d to sp3 and sp3d2
(b) sp3d to sp2 and sp3
(c) sp3d to sp3d2 and sp3d3
(d) sp3d2 to sp3 and sp3d
75. The group having isoelectronic species is:
(a) O2−, F−, Na+, Mg2+
(b) O−, F−, Na, Mg+
(c) O2−, F−, Na, Mg2+
(d) O−, F−, Na+, Mg2+
76. 100 mL O2 and H2 kept at same temperature and pressure. What is true about their number of molecules
(a) 
(b) 
(c)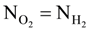 
(d) 
77. If mA gram of a metal A displaces mB gram of another metal B from its salt solution and if the equivalent mass are EA and EB respectively then equivalent mass of A can be expressed as:
(a) 
(b) 
(c) 
(d)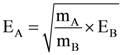 
78. Which one of the following set of quantum numbers is not possible for 4p electron?
(a) n = 4, l = 1, m = −1, ms = +1/2
(b) n = 4, l = 1, m = 0, ms = +1/2
(c) n = 4, l = 1, m = 2, ms = +1/2
(d) n = 4, l = 1, m = −1, ms = −1/2
79. Which of the following radial distribution graphs correspond to l = 2 for the H atom?
(a)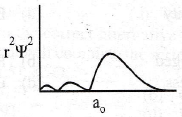 
(b) 
(c)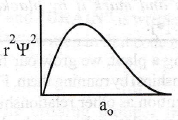 
(d)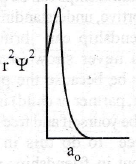 
80. Which of the following is paramagnetic?
(a) B2
(b) C2
(c) N2
(d) F2
PART-III(A): ENGLISH PROFICIENCY
DIRECTIONS (Qs. 81-83): In the following questions below, out of the four alternatives, choose the one which best expresses the meaning of the given word.
81. Garrulous
(a) Talkative
(b) Sedative
(c) Cocative
(d) Positive
82. Tinsel
(a) Tinkle
(b) Decoration
(c) Tin
(d) Colourful
83. Labyrinth
(a) Meandering
(b) Rotating
(c) Pacing
(d) Wriggling
DIRECTIONS(Qs .84-86) : In the following questions, choose the word opposite in meaning to the given word.
84. Knack:
(a) Talent
(b) Dullness
(c) Dexterity
(d) Balance
85. Pernicious:
(a) Prolonged
(b) Ruinous
(c) Ruthless
(d) Beneficial
86. Opulence :
(a) Luxury
(b) Transparency
(c) Wealth
(d) Poverty
DIRECTIONS (Qs. 87-90) : Read the passage carefully and choose the best answer to each question out of the four alternatives and mark it by blackening the appropriate circle [•].
Like watering a plant, we grow our friendships [and all our relationship) by running them, Friendships need the same attention as other relationships. If they are to continue. These relationships can be delightfully non-judgemental, supportive, understanding and fun.
Sometimes a friendship can bring out the positive side that you never show in any other relationship. This may be because the pressure of playing a ‘role’ (daughter, partner or child) is removed. With friend you are to be yourself and free to change. Of course, you are free to do this in all other relationships as well, but in friendships you get to have lats of rehearsals and discussion about changes as you experience them. It is an unconditional experience where you receive as much as you give. You can explain yourself to a friend openly without the fear of hurting a family member. How do friendships grow? The answer is simple. By revealing yourself; being attentive: remembering what is most showing empathy; seeing the world through the eyes of your friend, you will understand the value of friendship. All this means learning to accept a person from a completely different family to your own or perhaps someone from a completely different cultural background. This is the way we learn tolerance. In turn we gain tolerance and acceptance for our own differences.
87. In good friendships, we
(a) give and receive
(b) neither give nor receive
(c) only give
(d) only receive
88. Empathy means
(a) someone else’s misfortunes
(b) the ability to share and understand another feelings.
(c) skill and efficiency
(d) ability to do something
89. Through strong friendships, we gain
(a) only acceptance.
(b) only attention.
(c) acceptance and tolerance.
(d) only tolerance.
90. Friendships and relationships grow when they are
(a) compared
(b) divided
(c) favoured
(d) nurtured
DIRECTIONS (Qs. 91-92) In the following questions, sentences are given with blanks to be filled with an appropriate word(s). Four alternatives are suggested for each question. Choose the correct alternative out of the four as your answer.
91. There are not solitary, free-living creatures; every form of life is ______other forms.
(a) dependent on
(b) parallel to
(c) overshadowed by
(d) segregated from
92. I’ll take _____ now as I have another’s appointment some where else.
(a) departure
(b) your leave
(c) permission
(d) leave from work
DIRECTIONS(Qs. 93-95) : In the following questions, some parts of the sentences have errors and some are correct. Find out which part of a sentence has an error. The number of that part is the answer. If a sentence is free from error, then your answer is (d). i.e., No error.
93. When one hears of the incident (a)/about the plane crash(b)/ he feels very sorry. (c)/ No error (d)
94. I went there (a)/ with a view to survey (b)/ the entire procedure. (c)/No error (d)
95. It had laid(a)/in the closet(b)/ for a week before we found it. (c)/ No error(d)
PART-III(B) : LOGICAL REASONING
DIRECTIONS (Qs. 96 & 97) : In the following questions, which answer figure will complete the question figure?
96.
97.
98.
99. Select the related word from the given alternatives:
Medicine : Patient : Education :?
(a) Teacher
(b) School
(c) Student
(d) Tuition
100. Choose the correct alternative from the given ones that will complete the series.
A3E, F5J, K7O,_____
(a) Q11T
(b) Q9V
(c) P9T
(d) P11T
101. Which one of the following numbers lacks the common property in the series?
81, 36, 25, 9, 5, 16
(a) 5
(b) 9
(c) 36
(d) 25
102. In a certain code language, “TIRED” is written as “56” and “BRAIN” is written as “44”> How is “LAZY” written in that code language?
(a) 64
(b) 61
(c) 58
(d) 43
103. Select the missing number from the given response.
(a) 66
(b) 87
(c) 78
(d) 76
104. Which one of the following diagrams best depicts the relationship among Human Society – Youth Club, Political Party and Youths?
(a) 
(b) 
(c) 
(d) 
105. Among her children, Ganga’s favourites are Ram and Rekha. Rekha is the mother of Sharat, who is loved most by his uncle Mithun. The head of the family is Ram Lal, who is succeeded by his sons Gopoal and Mohan. Gopal and Ganga have been married for 35 years and have 3 children. What is the relation between Mithun and Mohan?
(a) Uncle
(b) Son
(c) Brother
(d) No relation
PART-IV : MATHEMATICS
106. If x cos α + y sin α = P is a tangent to the ellipse 
then
(a) a cos α + b sin α = P2
(b) a sin α + b cos α = P2
(c) a2 cos2 α + b2sin2 α = P2
(d) a2sin2 α + b2cos2 α = P2
107. If a1, a2, a3 …….., an are in A.P. where a1 > 0 for all i, then
(a)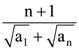 
(b) 
(c)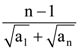 
(d) none of these
108. In order to solve the differential equation 
the integrating factor is:
(a) x cos x
(b) x sec x
(c) x sin x
(d) x cosec x
109. Equation of two straight lines are 
and 
. Then
(a) The lines are non-coplanar
(b) The lines are parallel and distinct
(c) The lines intersect in unique point
(d) The lines are coincident
110. The equation of the curve passing through the point (a, −1/a) and satisfying the differential equation 
is
(a) (x + a) (1 + ay) = −4a2y
(b) (x + a) (1 − ay) = 4a2y
(c) (x + a) (1 − ay) = −4a2y
(d) None of these
111. The locus of the mid-point of a chord of the circle x2 + y2 = 4, which subtends a right angle at the origin is
(a) x + y = 2
(b) x2 + y2 = 1
(c) x2 + y2 = 2
(d) x + y = 1
112. With the usual notation 
is equal to
(a) 4 + √2 − √3
(b) 4 − √2 + √3
(c) 4 − √2 – √3
(d) none of these
113. 
(a) 
(b) 
(c) 
(d) 
114. If 
(a) 
(b) 
(c) 
(d) 
115. If f(x) = 3x4 + 4x3 – 12x2 + 12, then f(x) is
(a) increasing in (–∞,–2) and in (0, 1)
(b) increasing in (–2, 0) and in (1, ∞)
(c) decreasing in (–2, 0) and in (0, 1)
(d) decreasing in (–∞,–2) and in (1, ∞)
116. Consider 
Then number of possible solutions are :
(a) Zero
(b) Unique
(c) Infinite
(d) None of these
117. The distance of a point (2, 5 –3) from the plane 
is
(a) 13
(b) 13/7
(c) 13/5
(d) 37/7
118. The value of definite integral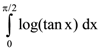 
is
(a) 0
(b) π/4
(c) π/2
(d) π
119. For the following feasible region, the linear constraints are
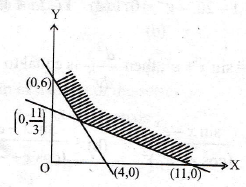
(a) x ≥ 0, y ≥ 0, 3x + 2y ≥ 12, x + 3y ≥ 11
(b) x ≥ 0, y ≥ 0, 3x + 2y ≤ 12, x + 3y ≥ 11
(c) x ≥ 0, y ≥ 0, 3x + 2y ≤ 12, x + 3y ≤ 11
(d) None of these
120. The general solution of differential equation (ex + 1) ydy = (y + 1) ex dx is
(a) (y + 1) = k(ex + 1)
(b) y + 1 = ex + 1 + k
(c) y = log {k(y + 1) (ex + 1)}
(d) 
121. What is the slope of the normal at the point (at2, 2at) of the parabola y2 = 4ax?
(a) 1/t
(b) t
(c) −t
(d) −1/t
122. 
is equal to
(a) π2/32
(b) π2/16
(c) π/32
(d) None of these
123. If 
, then what is x equal to?
(a) 3
(b) 2
(c) 1
(d) 0
- The limit
(a) is equal to 1/2
(b) is equal to −1/2
(c) is equal to 2
(d) does not exist
125. If 2 cos2 x + 3 sin x – 3 = 0, 0 ≤ x ≤ 180°, then x = 0
(a) 30°, 90°, 150°
(b) 60°, 120°, 180°
(c) 0°, 30°, 150°
(d) 45°, 90°, 135°
126. If the number of available constraints is 3 and the number of parameters to be optimized is 4, then
(a) The objective function can be optimized
(b) The constraint are short in number
(c) The solution is problem oriented
(d) None of these
127. If 
then y'(1) is equal to
(a) 0
(b) 1/2
(c) −1
(d) −1/4
128. The maximum area of rectangle inscribed in a circle of diameter R is
(a) R2
(b) R2/2
(c) R2/4
(d) R2/8
129. If A and B are two events, such that P (A ⋃ B) = 3/4, P(A ⋂ B) = 1/4, P(Ac) = 2/3 where A° stands for the complementary event of A, then P(B) is given by:
(a) 1/3
(b) 2/3
(c) 1/9
(d) 2/9
130. If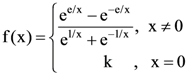 
then
(a) f is continuous at x, when k = 0
(b) f is not continuous at x = 0 for any real k.
(c) 
(d) None of these
131. 
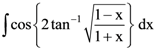is equal to
(a) 
(b) 
(c) 
(d) None of these
132. The equation of chord of the circle x2 + y2 = 8x bisected at the point (4, 3) is
(a) x = 3
(b) y = 3
(c) x = −3
(d) y = −3
133. x and y are positive number. Let g and a be G.M. and Am of these numbers. Also let G be G. M. of x + 1 and y + 1. If and g are roots of equation x2 – 5x + 6 = 0, then
(a) x = 2, y = 3/4
(b) x = 3/4, y = 12
(c) x = 5/2, y = 8/5
(d) x = y = 2
134. The co-efficient of xn in the expansion of 
(a)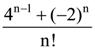 
(b) 
(c)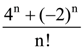 
(d)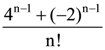 
135. A pair of tangents are drawn from the origin to the circle x2 + y2 + 20(x + y) + 20 = 0, then the equation of the pair of tangent are
(a) x2 + y2 – 5xy = 0
(b) x2 + y2 + 2x + y = 0
(c) x2 + y2 – xy + 7 = 0
(d) 2x2 + 2y2 + 5xy = 0
136. If the sum of a certain number of terms of the A.P. 25, 22, 19, …..is 116. then the last term is
(a) 0
(b) 2
(c) 4
(d) 6
137. If 1, a and P are in A.P. and 1, g and P are in G.P., then
(a) 1 + 2a + g2 = 0
(b) 1 + 2a – g2 = 0
(c) 1 – 2a – g2 = 0
(d) 1 – 2a + g2 = 0
138. If y = sin x + ex, then 
is equal to
(a) 
(b)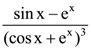 
(c)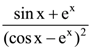 
(d) (−sin x + ex)−1
139. The foci of the hyperbola 4x2 – 9y2 – 1 = 0 are
(a) (±√13, 0)
(b) (±√13/6, 0)
(c) (0, ±√13/6)
(d) None of these
140. From the top of a cliff 50 m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 45°. The height of tower is
(a) 50 m
(b) 50√3 m
(c) 50(√3 – 1)m
(d)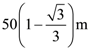 
141. The coefficient of x2 tem in the binomial expansion of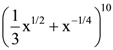 
is:
(a) 70/243
(b) 60/423
(c) 50/13
(d) none of these
142. The value of λ, for which the circle x2 + y2 + 2λr + 6y + 1 = 0 intersects the circle x2 + y2 + 4x + 2y = 0 orthogonally, is
(a) 11/8
(b) −1
(c) −5/4
(d) 5/2
143. The value of 
is
(a) 
(b) 
(c) 1
(d) None of these
144. If f(x) = a – xn)1/n, where a > 0 and n ∈ N, then fof(x) is equal to:
(a) a
(b) x
(c) xn
(d) an
145. Sum of n terms of the series 8 + 88 + 888 + … equals
(a) 
(b) 
(c) 
(d) None of these
146. The modulus of the complex number z such that |z + 3 – i| = 1 and arg(z) = π is equal to
(a) 3
(b) 2
(c) 9
(d) 4
147. Bag P contains 6 red and 4 blue balls and bag Q contains 5 red and 6 blue balls. A ball is transferred from bag P to bag Q and then a ball is drawn from bag Q. What is the probability that the ball drawn is blue?
(a) 7/15
(b) 8/15
(c) 4/19
(d) 8/19
148. The number of 4-digit number that can be formed with the digits, 1, 2, 3, 4 and 5 in which at least 2 digits are identical, is
(a) 505
(b) 45 – 5!
(c) 600
(d) None of these
149. Consider the system of linear equations;
x1 + 2x2 + x3 = 3
2x1 + 3x2 + x3 = 3
3x1 + 5x2 + 2x3 = 1
The system has
(a) exactly 3 solutions
(b) a unique solution
(c) no solution
(d) infinite solutions
150. What is the value of y so that the line through (3, y) and (2, 7) is parallel to the line through (−1, 4) and (0, 6)?
(a) 6
(b) 7
(c) 5
(d) 9