BITSAT SOLVED PAPER-2021
PART-I
PHYSICS
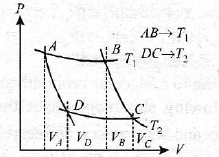
1. An ideal monoatomic gas is taken round the cycle of ABCDA as shown in the p-V diagram.
The work done during the cycle is
(a) pV
(b) 2pV
(c) pV/2
(d) zero
2. The initial speed of a body of mass 2.0 kg is 5 m/s. A force acts for 4 s in the direction of motion of the body, as shown in force-time graph. The impulse of force is
(a) 8.50 Ns
(b) 8 Ns
(c) 5.5 Ns
(d) 6 Ns
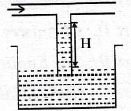
3. For a constant hydraulic stress on an object, the fractional change in the object’s volume (∆V/V) and its bulk modulus B are related as
4. A shunt is connected in parallel with a galvanometer. Why?
(a) To prevent galvanometer from strong current
(b) To convert galvanometer into ammeter
(c) To increase the range of ammeter
(d) All of the above
5. The phase difference between the Vout and Vin of CE-amplifier circuit is
(a) 90°
(b) 180°
(c) 0°
(d) 270°
6. If nth division of main scale coincides with (n + 1)th divisions of vernier scale. The least count of the vernier is (Given, one main scale division is equal to a units)
7. A uniform rod AB of length L = 1 m is sliding along two mutually perpendicular surfaces OP and OQ as shown in figure.
When the rod subtends an angle θ = 30° with OQ, then the end B has a velocity √3 m/s. The velocity of end A at that time is
(a) 1 m /s
(b) 0.5 m/s
(c) √3 m/s
(d) 1/√3 m/s
8. A tray of mass (M) 12 kg is supported by a spring as shown in figure.
When the tray is pressed down and released, it executes SHM with a period of 1.5 s. When a block of mass m placed on the tray, then the period of SHM changes to 3.0 s. The mass of block is
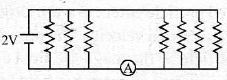
(a) 36 kg
(b) 48 kg
(c) 12 kg
(d) 24 kg
9. The phasor diagram of a load represents which circuit?
(a) Purely capacitive
(b) Purely inductive
(c) R-L-C circuit with XL more than XC
(d) R-L-C circuit with XL less than XC
10. The equation of progressive wave is given by Which one of the following is correct?
(a) υ = 5 cm/s
(b) λ = 18 cm
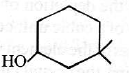
(c) A = 0.04 cm
(d) f = 50 Hz
11. The property of light used in optical fibre cable is
(a) total internal reflection
(b) refraction
(c) interference
(d) polarization
12. A man walks in a straight line for 5 mine with a velocity of 45 m/s. What is the speed with which he has to move in order to comeback to its original position in 1.5 min?
(a) 90 m/s
(b) 150 m/s
(c) 135 m/s
(d) 115 m/s
13. From a solid sphere of mass M and radius R, spherical portion of radius R/2 is removed as shown in the figure.
Taking gravitational potential V = 0 at r = ∞, the potential at the centre of the cavity thus formed is
(a) −GM/2R
(b) −GM/R
(c) −2GM/3R
(d) −2GM/R
14. Four charges equal to +Q are placed at the four corners of a square and a charge (−q) is at its centre. If the system is in equilibrium, then the value of –q is
15. A force F = a + bx acts on a particle in the x-direction, where a and b are constants. The work done by this force during a displacement from x =0 to x = d is
16. A proton has kinetic energy E = 100 eV which is equal to that of a photon. The wavelength of photon is λ2 and that of proton is λ1. The ratio λ2/λ1 is proportional to
(a) E2
(b) E1/2
(c) E−1
(d) E−1/2
17. A block of mass 10 kg rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and the plane is 0.1. The friction force on the block is
(a) 4.9 N
(b) 49√3 N
(c) 49 N
(d) 0.1 × 49√3 N
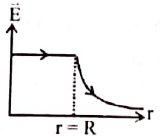
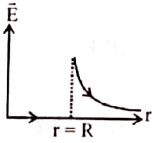
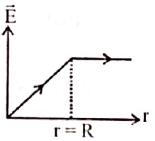
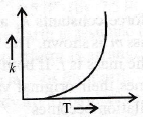
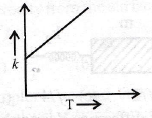
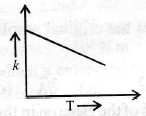
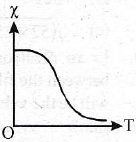
18. Which of the following graphs show the correct relation between conductivity and temperature for a metallic conductor?
19. The radius of a muonic hydrogen atom is 2.5 × 10−13 The total atomic volume (in m3) of a mole of such hydrogen atoms is
(Take, π = 3.14)
(a) 3.94 × 10−14
(b) 3.09 × 10−14
(c) 4 × 10−14
(d) 3.9 × 10−14
20. The angular momentum of a body placed at origin of mass 1 kg and having position vector is
(a) time dependent
(b)
(c)
(d) 0
21. If the earth stops rotating about its axis, then what will be the change in the value of g at a place in the equatorial plane?
(Radius of earth = 6400 km)
(a) 3.7 cm/s2
(b) 9.8 m/s2
(c) 0
(d) 3.4 cm/s2
22. Two cars approach a stationary observer from opposite sides as shown in the figure.
The observer hears to beats. If the frequency of the horn of the car B is 504 Hz, then the frequency of the horn of the car A will be
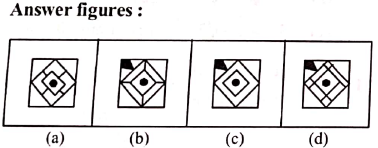
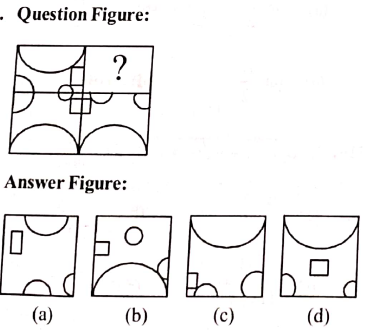
(a) 529.2 Hz
(b) 440.5 Hz
(c) 295.2 Hz
(d) None of these
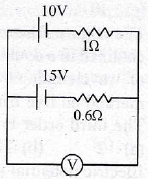
23.
In the following circuit, assuming point A to be at zero potential, then what is the potential at point B?
(a) 1 V
(b) 2 V
(c) 4 V
(d) 3 V
24. Two plane mirrors A and B are aligned parallel to each other as shown in the figure.
A ray of light is incident at an angle 30° at a point just inside one end of A. The plane of incidence coincides with the plane of the figure. The maximum number of times, the ray undergoes reflection (excluding the first one) before it emerges out is
(a) 28
(b) 34
(c) 30
(d) 29
25. A projectile is given an initial velocity of where
is along the ground and
is along the vertical. If g = 10 m/s2, then the equation of its trajectory is
(a) y = x + 5x2
(b) y = x – 5x2
(c) y = x2 + 5x
(d) y = x2 – 5x
26. Two drops of equal radius R coalesce to form a bigger drop. What is the ratio of surface energy of bigger drop to smaller one?
(a) 2−1/3; 1
(b) 22/3 : 1
(c) 1 : 1
(d) 21/2 : 1
27. Two particles A and B of masses mA and mB respectively, are having same charge and moving on same plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vA and vB respectively and the trajectories are as shown in figure. Then,
(a) mA = mB and vA = vB
(b) mAvA > mBvB
(c) mA < mB and vA < υB
(d) mAvA < mBvB
28. The potential difference applied to an X-ray tube is decreased. As a result, in the emitted radiation,
(a) the intensity increases
(b) the intensity decreases
(c) the minimum wavelength increases
(d) the minimum wavelength decreases
29. The ratio of the specific heats in terms of degrees of freedom n is given by
30. A cyclist speeding at 6 m/s in a circle of 18 m radius makes an angle θ with the vertical. The minimum possible value of coefficient of friction between the tyres and the ground is
(a) 12.041
(b) 0.2041
(c) 11.32
(d) 10.020
31. Three particles each of mass m are kept at the vertices of an equilateral triangle of side b. Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
(a) 3 mb2
(b) mb2
(c) mb2/3
(d)
32. An electric dipole is placed at an angle of 30° in a non-uniform electric field. The dipole will experience
(a) torque only
(b) translational force only in the direction of the field
(c) translational force only in a direction normal to the direction of the field
(d) torque as well as a translational force
33. Two coils A and B have a mutual inductance 0.001 H. The current changes in the first coil according to the equation i = i0 sin ωt, where i0 = 10A and ω = 10π rads−1. The maximum value of emf in the second coil is
(a) 0.01 π V
(b) 1 πV
(c) 0.1 π V
(d) 0.05 π V
34. The current in the circuit will be
(a) 0.125 A
(b) 0.1 A
(c) 0.5 A
(d) 0.25 A
35. The bob of a pendulum of length 2m lies at P, when it reaches Q, it loses 10% of its total energy due to air resistance.
The velocity of bob at Q is
(a) 6 m/s
(b) 1 m/s
(c) 2 m/s
(d) 8 m/s
36. A particle executes SHM with a frequency f. The frequency with which its kinetic energy oscillates is
(a) f/2
(b) f
(c) 2f
(d) 4f
37. A radioactive sample at any instant has its disintegration rate 5000 disintegrations per min. After 5 min, the rate is 1250 disintegrations per min. Then, the disintegration constant (per min) is
(a) 0.4 loge 2
(b) 0.2 loge 2
(c) 0.1 loge 2
(d) 0.8 loge 2
38. The separation between two parallel plates of capacitor is 1 mm. What is the electric potential generates between the plates of capacitor, when electric field of 2000 N/C is applied on it?
(a) 2 V
(b) 2000 V
(c) 0.2 V
(d) 200 V
39. Choose the correct statement.
(a) The speed of light in the meta-material is υ = c|n|.
(b) The speed of light in the meta-material is υ = c/|n|.
(c) The speed of light in the meta-material is υ = c.
(d) The wavelength of the light in the meta-material (λm) is given by λm = λair|n|.
40. A T-shaped object with dimensions shown in figure, is lying on a smooth floor. A force F is applied at the point P parallel to AB, such that the object has only the translational motion without rotation. Find the location of P with respect to C.
PART II
Chemistry
41. The most volatile compound among the given option is
(a) o-nitrophenol
(b) p-nitrophenol
(c) m-nitrophenol
(d) can’t say
42. What is the magnetic moment of Ti2+?
(Given : Atomic number = 22)
(a) √8
(b) √10
(c) √6
(d) √9
43. Why only Xe can form compounds with fluorine among noble gases?
(a) Large size
(b) Low electronegativity
(c) High ionization energy
(d) Low electron gain enthalpy
44. Which of the following inert gas is used as cryogenic agent?
(a) He
(b) Ne
(c) Ar
(d) Kr
45. For the following reaction,
2A + 3B → 3C + 4D
Expression for rate of reaction is
46. Cyclohexanol on reacting with H2SO4 and then heating gives
(a) cyclohexene
(b) cyclohexanone
(c) cyclohexanol
(d) None of these
47. The major product obtained on reaction of 3-methylbutene with HCl is
(a) 2-chloro-2-methylbutane
(b) 3-chloro-2-methylbutane
(c) 1-chloro-2-methylbutane
(d) 3-chloro-3-methylbutane
48. If Rydberg constant is same for all elements, the angular momentum and energy of Li2+ of which orbital is equal to angular momentum and energy of 1s-orbital of hydrogen atom?
(a) 3s
(b) 4s
(c) 2p
(d) 3d
49. Sodium iodide reacts with ammonia to give
(a) [Na(NH3)4]I
(b) [Na(NH3)4]I3
(c) [Na(NH3)I3]I
(d) [Na(NH3)3I]
50. In photography, which compound is used as a fixing agent
(a) sodium thiosulphate
(b) ammonium thiosulphate
(c) sodium chloride
(d) Both (a) and (b)
51. The compound formed on reaction of epoxy ethane with NH3 and H2O is
(a) mono-ethanol amines
(b) di-ethanol amines
(c) tri-ethanol amines
(d) All of these
52. The process of removal of excess electrolyte from colloidal solution is
(a) coagulation
(b) dialysis
(c) ultra-filtration
(d) peptisation
53. Maltase converts maltose into
(a) glucose
(b) sucrose
(c) fructose
(d) starch
54. Starch is a polymer of
(a) glucose
(b) fructose
(c) Both (a) and (b)
(d) None of these
55. Methyl alcohol can be distinguished from ethyl alcohol using
(a) Fehling solution
(b) Schiff’s reagent
(c) Sodium hydroxide and iodine
(d) Phthalein fusion test
56. Sodium stearate (C17H35COO−Na+) is
(a) anionic soap
(b) cationic detergent
(c) anionic detergent
(d) Non-ionic soap
57. Which is not an anti-fluorite structure
(a) Rb2S
(b) BaF2
(c) K2O
(d) Li2O
58. The structure of ClF3 is
(a) T-shape
(b) bent shape
(c) linear
(d) trigonal planar
59. Which of the following is diamagnetic in nature?
(a) O2
(b) O22−
(c) N22+
(d) B2
60. The correct order of bond order in SO2, SO3, SO42−, SO32− is
(a) SO32− > SO42− > SO3 = SO2
(b) SO42− > SO3 > SO2 > SO32−
(c) SO2 = SO3 > SO42− > SO32−
(d) Can’t say
61. Ionisation energy for H+ ion is proportional to rn, then value of n is
(a) 1
(b) −1
(c) 2
(d) −2
62. Role of BHA in food industries
(a) prevent oxidation
(b) prevent reduction
(c) add sweeteners
(d) None of these
63. Permanganate ion (MnO4−) is dark purple coloured though Mn is in +7 oxidation state with d0 This is due to
(a) d – d transition
(b) charge transfer from metal to ligand
(c) charge transfer from ligand to metal
(d) All of the above
64. Rutherford model could not explain
(a) electronic structure of an atom
(b) stability of an atom
(c) Both (a) and (b)
(d) None of the above
65. Which is true in case of [Ni(CO)4]?
(a) Hybridization of Ni is sp3
(b) Hybridization of Ni is dsp2
(c) Paramagnetic
(d) Square planar
66. SI unit of Boltzmann’s constant is
(a) JK−1
(b) eVK−1
(c) ergK−1
(d) JK
67. Acetone does not undergo which type of reaction?
(a) Substitution reaction
(b) Polymerization reaction
(c) Condensation reaction
(d) Addition reaction
68. Magnetic moment of Co in [CoF6]2− of unpaired electron is
(a) √35
(b) √45
(c) √40
(d) √30
69. Some statement about heavy water are given below
(1) Heavy water is used as a moderator in nuclear
(2) Heavy water is more associated than ordinary water.
(3) Heavy water in more effective solvent than ordinary water.
Which of the above statements are correct?
(a) 1 and 2
(b) 1, 2 and 3
(c) 2 and 3
(d) 1 and 3
70. CH3−CHCl−CH2−C3 has a chiral centre, which of the following represents its R configuration?
71. In Victor Meyer’s method 0.2 g of an organic substance displaced 56 mL of air at STP the molecular weight of the compound is
(a) 56
(b) 112
(c) 80
(d) 28
72. For the complete combustion of ethanol, C2H5OH(l) + 3O2(g) → 2CO2(g) + 3H2O(l)the amount of heat produced as measured in bomb calorimeter is 1364.47 kJ mol−1 at 25° Assuming ideality the enthalpy of combustion, ∆HC, for the reaction will be
(R = 8.314 JK−1 mol−1)
(a) −1366.95 kJ mol−1
(b) −1361.95 kJ mol−1
(c) −1460.50 kJ mol−1
(d) −1350.50 kJ mol−1
73. The incorrect expression among the following is
(a)
(b) In isothermal process,
(c)
(d)
74. The solubility of Pb(OH)2 in water is 6.7 × 10−6 Its solubility in a buffer solution of pH = 8 would be
(a) 1.2 × 10−2
(b) 1.6 × 10−3
(c) 1.6 × 10−2
(d) 1.2 × 10−3
75. The density (in g mL−1) of a 60 M sulphuric acid solution that is 29% H2SO4 (molar mass = 98 g mol−1) by mass will be
(a) 1.64
(b) 1.88
(c) 1.22
(d) 1.45
76. The relative lowering of vapour pressure of a dilute aqueous solution containing non-volatile solute is 0.0125. The molality of the solution is about
(a) 0.70
(b) 0.50
(c) 0.90
(d) 0.80
77. Equal masses of methane and oxygen are mixed in an empty container at 25° The fraction of the total pressure exerted by oxygen is
(a) 2/3
(b)
(c) 1/3
(d) 1/2
78. The molar conductivities of KCl NaCl and KNO3 are 152, 128 and 111 S cm2 mol−1 What is the molar conductivity of NaNO3?
(a) 101 S cm2 mol−1
(b) 87 S cm2 mol−1
(c) −101 S cm2 mol−1
(d) −391 S cm2 mol−1
79. The approximate time duration in hours to electroplate 30 g of calcium form molten calcium chloride using a current of 5 A is (Atomic mass of Ca = 40)
(a) 80
(b) 10
(c) 16
(d) 8
80. Given, the reduction potential of Na+, Mg2+, Al3+ and Ag+ as
The least stable oxide is
(a) Ag2O
(b) Al2O3
(c) MgO
(d) Na2O
PART III
(a) English Proficiency
Directions (Q. Nos. 81-83) Choose the word which best expresses the meaning of the underlined word in the sentence.
81. Decay is an immutable factor of human life.
(a) important
(b) unique
(c) unchangeable
(d) awful
82. It was an ignominious defect for the team.
(a) shameful
(b) admirable
(c) unaccountable
(d) worthy
83. His conjecture was the better than mine.
(a) guess
(b) fact
(c) surprise
(d) doubt
Directions (Q. Nos. 84-86) Fill in the blanks.
84. Freedom and equality are the ………. Rights of every human.
(a) inalienable
(b) inscrutable
(c) incalculable
(d) institutional
85. Pradeep’s face spoke …………. of the happiness he was feeling.
(a) elegantly
(b) tons
(c) volumes
(d) much
86. His speech was disappointing : it …………. All the major issues.
(a) projected
(b) revealed
(c) skirted
(d) analysed
Directions (Q. Nos. 87-89) Choose the word which is closest to the opposite in meaning of the given italicized word.
87. Hydra is biologically believed to be immortal.
(a) undying
(b) perishable
(c) ancient
(d) eternal
88. The Gupta rulers patronized all cultural activities and thus Gupta period was called the golden era in Indian History.
(a) criticized
(b) rejected
(c) opposed
(d) spurned
89. This is a barbarous
(a) bad
(b) good
(c) civilized
(d) exemplary
Directions (Q. Nos. 90-92) In each of the following questions, out of the four alternatives, choose the one which can be substituted for the given words/sentence.
90. A person who does not believe in any religion
(a) Philatelist
(b) Rationalist
(c) Atheist
(d) Pagan
91. A person who believes that pleasure is the chief good
(a) Stoic
(b) Hedonist
(c) Epicure
(d) Sensual
92. One who loves mankind
(a) Anthropologist
(b) Philanthropist
(c) Seismologist
(d) Optometrist
Directions (Q. Nos. 93-95) Choose the order of the sentence marked A, B, C, D and E to form a logical paragraph.
93. (A) Tasty and healthy food can help you bring out their best.
(B) One minute they are toddlers and next you see them in their next adventure.
(C) Your young ones seem to be growing so fast.
(D) Being their loving custodians, you always want to see them doing well.
(E) Their eyes sparkle with curiosity and endless questions on their tongues.
Codes
(a) DBCEA
(b) CADEB
(c) CBEDA
(d) ECABD
94. (A) It is hoping that overseas friends will bring in big money and lift the morale of the people.
(B) But a lot needs to be done to kick start industrial revival.
(C) People had big hopes from the new government.
(D) So far government has only given an incremental push to existing policies and programmes.
(E) Government is to go for big time reforms, which it promised.
Codes
(a) BCDAE
(b) EADCB
(c) DABEC
(d) CDEAB
95. (A) However, women hiring is catching up at a slow and steady rate in the recent times.
(B) Gender ratio has been inclined more towards male employees.
(C) As a result, recent reports have highlighted the rise in demand for women employees.
(D) Women constitute a little over half of world’s total population.
(E) But, their contribution to measured economic activity is far below the potential.
Codes
(a) DEBAC
(b) CDAEB
(c) BCDEA
(d) AEDBC
(b) Logical Reasoning
96. Choose the correct answer figure which will make a complete square on joining with the problem figure.
97. In the following question, five figures are given. Out of them, find the three figures that can be joined to form a square.
98. Choose the answer figure which completes the problem figure matrix.
99. From the given four positions of a single dice, find the colour at the face opposite to the face having red colour.
100. In the following questions, one or more dots are placed in the figure marked as (A). The figure is followed by four alternatives marked as (a), (b), (c) and (d). One out of these four options contains region(s) common to the circle, square, triangle, similar to that marked by the dot in figure (A).
101. Complete the series by replacing ‘?’ mark.
G4T, J9R, M20P, P43N, S90L, ?
(a) S90L
(b) V185J
(c) M20P
(d) P43N
102. Neeraj starts walking towards South. After walking 15 m, he turns towards North. After walking 20 m, he turns towards East and walks 10 m. He then turns towards South and walks 5 m. How far is he from his original position and in which direction?
(a) 10 m, East
(b) 10 m, South-East
(c) 10 m, West
(d) 10 m, North-East
103. The average age of 8 men is increased by 2 yrs. when one of them whose age is 20 yr is replaced by a new man. What is the age of the new man?
(a) 28 y r
(b) 36 yr
(c) 34 yr
(d) 35 yr
104. Shikha is mother-in-law of Ekta who is sister-in-law of Ankit. Pankaj is father of Sanjay, the only brother of Ankit. How is Shikha related to Ankit?
(a) Mother-in-law
(b) Aunt
(c) Wife
(d) Mother
105. In a row of forty children, P is thirteenth from the left end and Q is ninth from the right end. How many children are there between P and R, if R is fourth to the left of Q?
(a) 12
(b) 13
(c) 14
(d) 15
PART IV
Mathematics
106. If Re(z + 2) = |z – 2|, then the locus of z is
(a) parabola
(b) circle
(c) ellipse
(d) hyperbola
107. If a ∈ R, b ∈ R, then the equation
x2 – abx – a2 = 0 has
(a) one positive root and one negative root
(b) Both positive roots
(c) Both negative roots
(d) Non-real roots
108. If a + 2b + 3c = 12 (a, b, c ∈ R+), then the maximum value of ab2c3 is
(a) 23
(b) 24
(c) 26
(d) 25
109. Sum of n terms of the infinite series
1.32 + 2.52 + 3.72 + … ∞ is
110. If log7 5 = a, log5 3 = b and log3 2 = c, then the logarithm of the number 70 to the base 225 is
111. The maximum number of points of intersection of 10 circles is
(a) 80
(b) 90
(c) 85
(d) 95
112.
(a) 120
(b) 260
(c) 210
(d) 180
113. If p ≠ q ≠ r and then the value of x which satisfy the equation is
(a) x = p
(b) x = q
(c) x = r
(d) x = 0
114. Matrix if xyz = 60 and 8x + 4y + 3z = 20, then A(adj A) is equal to
115. If f(x) = 4x – x2, x ∈ R, and f(a + 1) – f(a – 1) = 0, then a is equal to
(a) 0
(b) 2
(c) 1
(d) 3
116. Which of the following is not an equivalence relation in z?
(a) aRb ⇔ a + b is an even integer
(b) aRb ⇔ a − b is an even integer
(c) aRb ⇔ a < b
(d) aRb ⇔ a = b
117. Which of the following is always true?
(a) (~ p ˅ ~ q) ≡ (p ˄ q)
(b) (p → q) ≡ (~ p → ~ p)
(c) ~(p → ~ q) ≡ (p ˄ ~ q)
(d) ~(p ⟷ q) ≡ (p → q) → (q → p)
118. The solution of the inequation 4−x + 0.5 – 7.2−x < 4, x ∈ R is
(a) (−2, ∞)
(b) (2, ∞)
(c) (2, 7/2)
(d) None of these
119. If is identity in x, then
(a) a3 = 3/8, a2 = 0
(b) n =6, a1 = 1/2
(c) n = 5, a1 = 3/4
(d) ∑am = 1/4
120. Total number of solutions of x ∈ [0, 3π] is equal to
(a) 1
(b) 2
(c) 3
(d) 0
121. The minimum value of (sin−1 x)3 + (cos−1 x)3 is equal to
(a) π3/32
(b) 5π3/32
(c) 9π3/32
(d) 11π3/32
122. The origin is shifted to (1, 2). The equation y2 – 8x – 4y + 12 = 0 changes to y2 = 4ax, then a is equal to
(a) 1
(b) 2
(c) −2
(d) −1
123. The equations of the bisector of the angles between the straight lines 3x + 4y + 7 = 0 and 12x + 5y – 8 = 0 are
(a) 7x + 9y + 17 = 0, 99x + 77y + 51 = 0
(b) 7x – 9y – 17 = 0, 99x + 77y – 51 = 0
(c) 7x – 9y + 17 = 0, 99x + 77y + 51 = 0
(d) None of the above
124. Equation of circle which passes through the points (1, −2) and (3, −4) and touch the X-axis is
(a) x2 + y2 + 6x + 2y + 9 = 0
(b) x2 + y2 + 10x + 20y + 25 = 0
(c) x2 + y2 + 6x + 4y + 9 = 0
(d) None of the above
125. If x = 9 is the chord of contact of the hyperbola x2 – y2 = 9, then the equation of the corresponding pair of tangent is
(a) 9x2 – 8y2 + 18x – 9 = 0
(b) 9x2 – 8y2 – 18x + 9 = 0
(c) 9x2 – 8y2 – 18x – 9 = 0
(d) 9x2 – 8y2 + 18x + 9 = 0
126. The points with position vectors and
are collinear, if a is
(a) −8
(b) 4
(c) 2
(d) 82/9
127. Let a, b, c be vectors of lengths 3, 4, 5 respectively and a be perpendicular to (b + c), to (c + a) and c to (a + b), then the value of (a + b + c) is
(a) 2√5
(b) 2√2
(c) 10√5
(d) 5√2
128. For non-zero vectors, a, b, c; |(a × b) ∙ c| = |a| |b| |c| holds if and only if
(a) a ∙ b = 0, b ∙ c = 0
(b) b ∙ c = 0, c ∙ a = 0
(c) c ∙ a = 0, a ∙ b = 0
(d) a ∙ b = b ∙ c = c ∙ a = 0
129. Angle between the diagonals of a cube is
(a) π/3
(b) π/2
(c) cos−1(1/3)
(d) cos−1(1/√3)
130. Consider the two lines
The unit vector perpendicular to both the lines L1 and L2 is
131. The distance between the line and the plane
is
(a) 10/9
(b) 10/3√3
(c) 10/3
(d) None of these
132. Two cards are drawn from a pack of 52 cards. What is the probability that either both are red or both are kings?
(a) 7/13
(b) 63/221
(c) 55/221
(d) 3/26
133. If A and B are two independent events such that P(A) = 1/2 and P(B) = 1/5, then which of the following is correct?
134. Box 1 contains 5 red and 2 blue balls, while box II contains 2 red and 6 blue balls. A fair coin is tossed. If it turns up head, a ball is drawn from box I, else a ball is drawn from box II. The probability ball drawn is from box I, if it is blue, is
(a) 27/56
(b) 8/29
(c) 21/29
(d) 29/56
135. For a random variable X, E(X) = 3 and E(X2) = 11. The variable of X is
(a) 8
(b) 5
(c) 2
(d) 1
136. The sum of 10 items is 12 and the sum of their squares is 18, then the standard deviation will be
(a) −3/5
(b) 6/5
(c) 4/5
(d) 3/5
137. The height of the chimney when it is found that on walking towards it 50 m in the horizontal line through its base, the angle of elevation of its top changes from 30° to 60° is
(a) 25 m
(b) 25√2 m
(c) 25√3 m
(d) None of these
138. The value of is
(a) 1/2
(b) 2
(c) √2
(d) None of these
139. If is differentiable at x = 1, then
(a) a = 1, b = 1
(b) a = 1, b = 0
(c) a = 2, b = 0
(d) a = 2, b = 1
140. The slope the tangent to the curve x = t2 + 3t – 8 y = 2t2 – 2t – 5 at the point t = 2 is
(a) 7/6
(b) 5/6
(c) 6/7
(d) 1
141. is equal to
142. is equal to
143. The area of one curvilinear triangle formed by curves y = sin x, y = cos x and X-axis, is
(a) 2 sq units
(b) (2 + √2) sq units
(c) (2 – √2) sq units
(d) None of the above
144. Solution of given that y = 1 when x = 1 is
145. If is
(a) 1
(b) −1
(c)
(d)
146. The maximum value of the function y = x(x – 1)2, is
(a) 0
(b) 4/27
(c) −4
(d) None of these
147. The solution of satisfying y(1) = 0, is
(a) tan y = (x – 2)ex log x
(b) sin y = ex(x – 1) x−1
(c) tan y = (x – 1)ex x−3
(d) sin y = ex(x – 1)x−3
148. The runs of two players for 10 innings each are as follows
The more consistent player is
(a) player A
(b) player B
(c) both player A and B
(d) None of the above
149. The linear programming problem minimize z = 3x + 2y subject to constraints x + y ≥ 8, 3x + 5y ≤ 15, x ≥ 0 and y ≥ 0, has
(a) one solution
(b) no feasible solution
(c) two solutions
(d) infinitely many solution
150. Find the area enclosed by the loop in the curve 4y2 = 4x2 – x3.
(a) 128/5
(b) 15/128
(c) 130/17
(d) 17/130

 in terms of degrees of freedom (n) given by
in terms of degrees of freedom (n) given by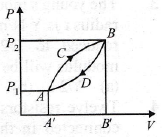




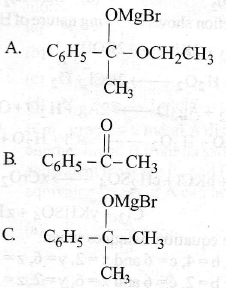

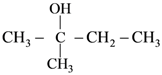

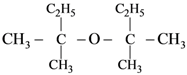


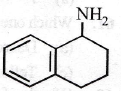


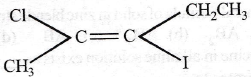
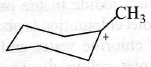

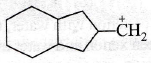

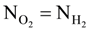
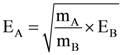
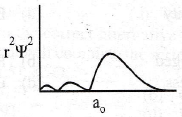








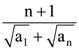

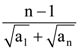
 is
is is equal to
is equal to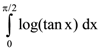 is
is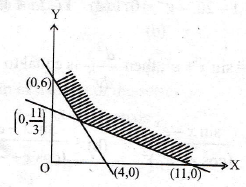

 is equal to
is equal to , then what is x equal to?
, then what is x equal to? then y'(1) is equal to
then y'(1) is equal to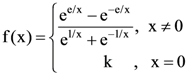 then
then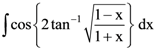 is equal to
is equal to
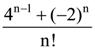

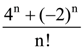
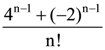

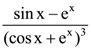
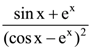
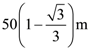
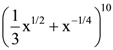 is:
is: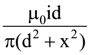


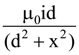

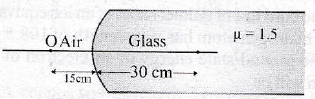



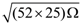
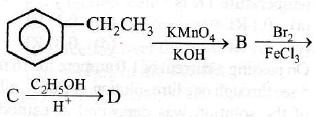
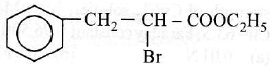

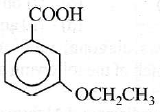





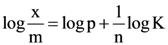
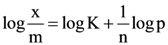
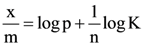

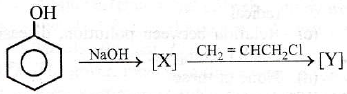
 (4) CH3OH
(4) CH3OH




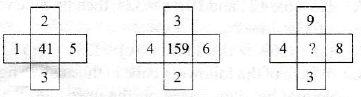


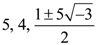
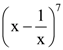 is:
is: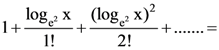
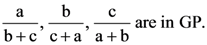
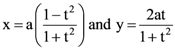 represent (t being a parameter)
represent (t being a parameter) if it passes through point (9, 5) and (12, 4) is
if it passes through point (9, 5) and (12, 4) is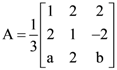 is an orthogonal matrix, then
is an orthogonal matrix, then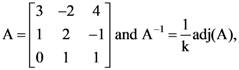 then k is
then k is then ∆ is
then ∆ is
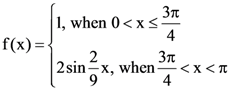
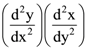 is
is is:
is: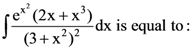


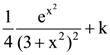
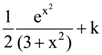
 then
then 
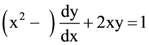
 is equal to
is equal to