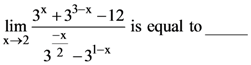Physics
Section-A
1. Match List I with List II.
List I
(a) Rectifier
(b) Stabilizer
(c) Transformer
(d) Filter
List II
(i) Used either for stepping up or stepping down the A.C. voltage
(ii) Used to convert A.C. voltage into D.C. voltage
(iii) Used to remove any ripple in the rectified output voltage
(iv) Used for constant output voltage even when the input voltage or load current change
Choose the correct answer form the options given below:
(a) (a)-(ii), (b)- (i), (c)-(iv), (d)-(iii)
(b) (a)-(ii), (b)- (iv), (c)-(i), (d)-(iii)
(c) (a)-(ii), (b)- (i), (c)-(iii), (d)-(iv)
(d) (a)-(iii), (b)- (iv), (c)-(i), (d)-(ii)
2. Y = A sin(ωt + ϕ0) is the time – displacement equation of an SHM, At t = 0, the displacement of the particle is Y = A/2 and it is moving along negative x-direction. Then, the initial phase angle ϕ0 will be.
(a) π/6
(b) π/3
(c) 2π/3
(d) 5π/6
3. Two identical springs of spring constant ‘2K’ are attached to a block of mass m and to fixed support (see figure). When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. Then, time period of oscillations of this system is:

(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
4. The wavelength of the photon emitted by a hydrogen atom when an electron makes a transition from n = 2 to n = 1 state is:
(a) 194.8 nm
(b) 490.7 nm
(c) 913.3 nm
(d) 121.8 nm
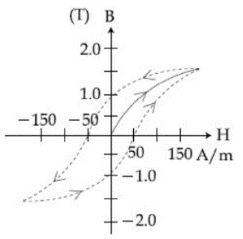
5. In a ferromagnetic material below the Curie temperature, a domain is defined as:
(a) a macroscopic region with consecutive magnetic diploes oriented in opposite direction.
(b) a macroscopic region with zero magnetization.
(c) a macroscopic region with saturation magnetization.
(d) a macroscopic region with randomly oriented magnetic dipoles.
6. The point A moves with a uniform speed along the circumference of a circle of radius 0.36m and cover 30° in 0.1s. The perpendicular projection ‘P’ form ‘A’ on the diameter MN represents the simple harmonic motion of ‘P’. The restoring force per unit mass when P touches M will be:

(a) 100 N
(b) 50 N
(c) 9.87 N
(d) 0.49 N
7. The stopping potential for electrons emitted from a photosensitive surface illuminated by light of wavelength 491 nm is 0.710 V. When the incident wavelength is changed to a new value, the stopping potential is 1.43 V. The new wavelength is:
(a) 400 nm
(b) 382 nm
(c) 309 nm
(d) 329 nm
8. A charge ‘q’ is placed at one corner of a cube as shown in figure. The flux of electrostatic field ![]() through the shaded area is:
through the shaded area is:

(a) q/48ε0
(b) q/8ε0
(c) q/24ε0
(d) q/4ε0
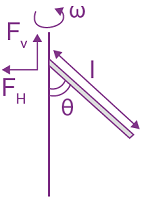
9. A sphere of radius ‘a’ and mass ‘m’ rolls along horizontal plane with constant speed v0. It encounters an inclined plane at angle θ and climbs upward. Assuming that it rolls without slipping how far up the sphere will travel (along the incline)?

(a) 
(b) 
(c) 
(d) 
10. Consider the diffraction pattern obtained from the sunlight incident on a pinhole of diameter 0.1 μm. If the diameter of the pinhole is slightly increased, it will affect the diffraction pattern such that:
(a) its size decreases, but intensity increases
(b) its size increases, but intensity decreases
(c) its size increases, and intensity increases
(d) its size decreases, and intensity decreases
11. An electron of mass me and a proton of mass mp = 1836 me are moving with the same speed. The ratio of their de Broglie wavelength ![]() will be:
will be:
(a) 918
(b) 1836
(c) 1/1836
(d) 1
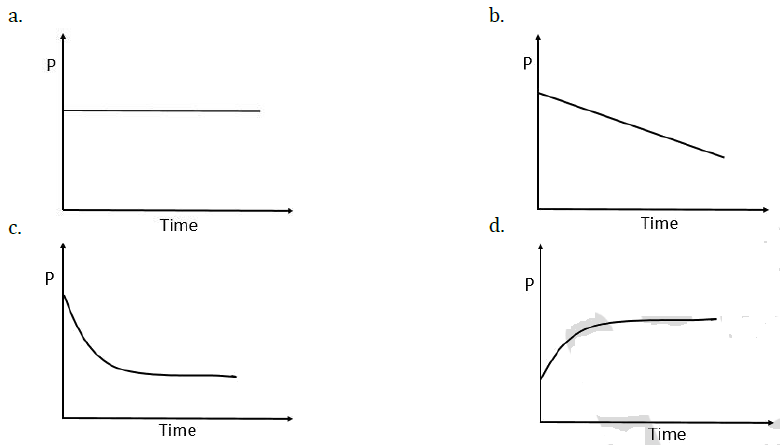
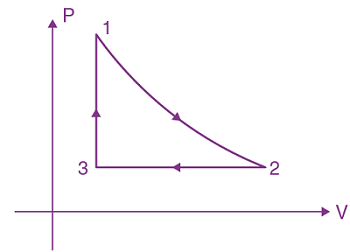
12. Thermodynamic process is shown below on a P-V diagram for one mole of an ideal gas. If V2 = 2V1 then the ratio of temperature T2/T1 is:

(a) 1/√2
(b) 1/2
(c) 2
(d) √2
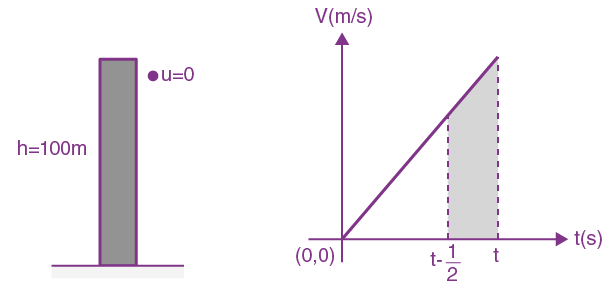
13. A stone is dropped from the top of a building. When it crosses a point 5m below the top, another stone starts to fall from a point 25m below the top, both stones reach the bottom of building simultaneously. The height of the building is: [Take g = 10 m/s2]
(a) 45 m
(b) 35 m
(c) 25 m
(d) 50 m
14. If a message signal of frequency ‘fm‘ is amplitude modulated with a carrier signal of frequency ‘fc‘ and radiated through an antenna, the wavelength of the corresponding signal in air is:
[Given, C is the speed of electromagnetic waves in vacuum/air]
(a) 
(b) 
(c) c/fm
(d) c/fc
15. Given below are two statements:
Statement I: In a diatomic molecule, the rotational energy at a given temperature obeys Maxwell’s distribution.
Statement II: In a diatomic molecule, the rotational energy at a given temperature equals the translational kinetic energy for each molecule.
In the light of the above statements, choose the correct answer from the options given below:
(a) Both statement I and statement II are false.
(b) Both statement I and statement II are true.
(c) Statement I is false but statement II is true.
(d) Statement I is true but statement II is false.
16. An electron with kinetic energy K1 enters between parallel plates of a capacitor at an angle ‘α’ with the plates. It leaves the plates at angle ‘β’ with kinetic energy K2. Then the ratio of kinetic energies K1 : K2 will be:
(a) 
(b) 
(c) ![]()
(d) ![]()
17. An LCR circuit contains resistance of 110 Ω and a supply of 220 V at 300 rad/s angular frequency. If only capacitance is removed from the circuit, current lags behind the voltage by 45°. If on the other hand, only inductor is removed the current leads by 45° with the applied voltage. The rms current flowing in the circuit will be:
(a) 2.5 A
(b) 2 A
(c) 1 A
(d) 1.5 A
18. For extrinsic semiconductors: when doping level is increased;
(a) Fermi–level of p and n-type semiconductors will not be affected.
(b) Fermi–level of p-type semiconductors will go downward and Fermi–level of n-type semiconductor will go upward.
(c) Fermi–level of both p–type and n–type semiconductors will go upward for T > TFK and downward for T < TFK, where TF is Fermi temperature.
(d) Fermi–level of p-type semiconductor will go upward and Fermi–level of n–type semiconductors will go downward.
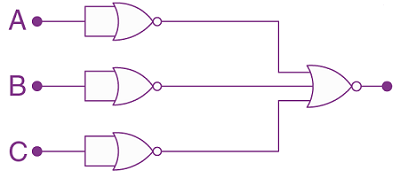
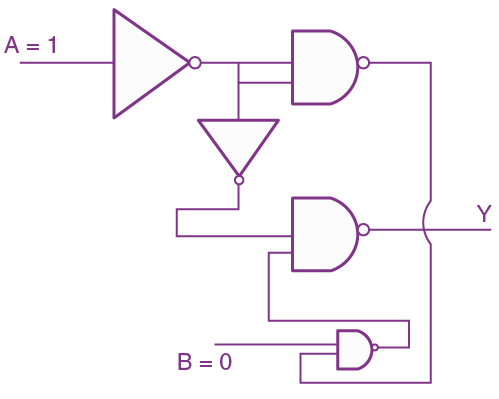
19. The truth table for the following logic circuit is:

(a) 
(b) 
(c) 
(d) 
20. If e is the electronic charged, c is the speed of light in free space and h is planck’s constant, the quantity  has dimensions of :
has dimensions of :
(a) [LC−1]
(b) [M0 L0 T0]
(c) [M L T0]
(d) [M L T−1]
Section-B
21. The percentage increase in the speed of transverse waves produced in a stretched string if the tension is increased by 4% will be _______%.
22. Two small spheres each of mass 10 mg are suspended from a point by threads 0.5 m long. They are equally charged and repel each other to a distance of 0.20 m. Then charge on each of the sphere is  The value of ‘a’ will be________. [Take g = 10 m/s2]
The value of ‘a’ will be________. [Take g = 10 m/s2]
23. The peak electric field produced by the radiation coming from the 8 W bulb at a distance of 10 m is  The efficiency of the bulb is 10% and it is a point source. The value of x is ___.
The efficiency of the bulb is 10% and it is a point source. The value of x is ___.
24. Two identical conducting spheres with negligible volume have 2.1nC and -0.1nC charges, respectively. They are brought into contact and then separated by a distance of 0.5 m. The electrostatic force acting between the spheres is _______× 10−9 [Given : ![]() SI unit]
SI unit]
25. The initial velocity v1 required to project a body vertically upward from the surface of the earth to just reach a height of 10R, where R is the radius of the earth, may be described in terms of escape velocity ve such that  The value of x will be _______.
The value of x will be _______.
26. A current of 6A enters one corner P of an equilateral triangle PQR having 3 wires of resistance 21Ω each and leaves by the corner R. The currents i1 in ampere is______.

27. The wavelength of an X-ray beam is 10 Å. The mass of a fictitious particle having the same energy as that of the X-ray photons is ![]() The value of x is _______.
The value of x is _______.
28. A reversible heat engine converts one- fourth of the heat input into work. When the temperature of the sink is reduced by 52 K, its efficiency is doubled. The temperature in Kelvin of the source will be_______.
29. Two particles having masses 4g and 16g respectively are moving with equal kinetic energies. The ratio of the magnitudes of their linear momentum is n:2. The value of n will be_____.
30. If ![]() the angle between
the angle between ![]() is θ(0° < θ < 360°). The value of ‘θ’ will be _______.
is θ(0° < θ < 360°). The value of ‘θ’ will be _______.
Chemistry
Section-A
1. Given below are two statements:
Statement I: The identification of Ni2+ is carried out by dimethylglyoxime in the presence of NH4OH
Statement II: The dimethylglyoxime is a bidentate neutral ligand.
In the light of the above statements, choose the correct answer from the options given below:
(a) Both statement I and statement II are true
(b) Both statement I and statement II are false
(c) Statement I is false but statement II is true
(d) Statement I is true but statement II is false
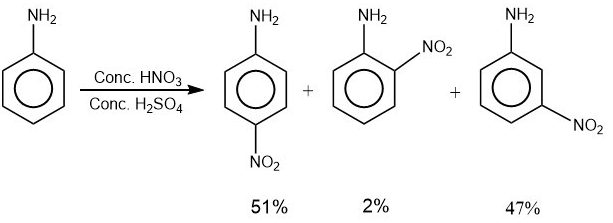
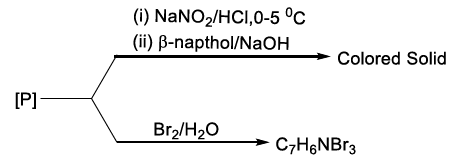
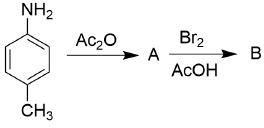
2. Carbylamine test is used to detect the presence of a primary amino group in an organic compound. Which of the following compounds is formed when this test is performed with aniline?

3. The correct order of bond dissociation enthalpy of halogen is:
(a) F2 > Cl2 > Br2 > I2
(b) Cl2 > F2 > Br2 >I2
(c) Cl2 > Br2 > F2 >I2
(d) I2 > Br2 > Cl2 > F2
4. Which one of the following statements is FALSE for hydrophilic sols?
(a) These sols are reversible in nature
(b) The sols cannot be easily coagulated
(c) They do not require electrolytes for stability
(d) Their viscosity is of the order of that of H2O
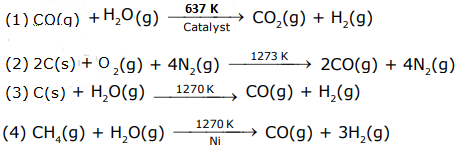
5. Water does not produce CO on reacting with
(a) C3H8
(b) C
(c) CH4
(d) CO2
6. What is ‘X’ in the given reaction?

7. If which of the following orders the given complex ions are arranged correctly with respect to their decreasing spin only magnetic moment?
(i) [FeF6]3−
(ii) [Co(NH3)6]3+
(iii) [NiCl4] 2−
(iv) [Cu(NH3)4]2+
(a) (ii) > (i) > (iii) > (iv)
(b) (iii) > (iv) > (ii) > (i)
(c) (ii) > (iii) > (i) > (iv)
(d) (i) > (iii) > (iv) > (ii)
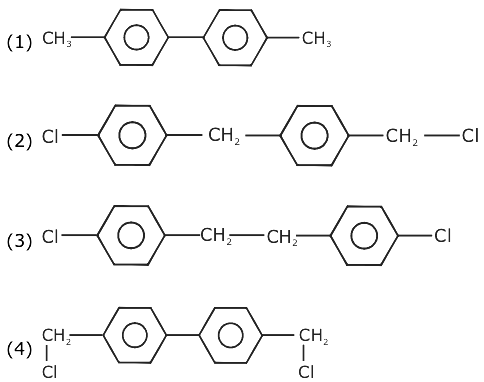
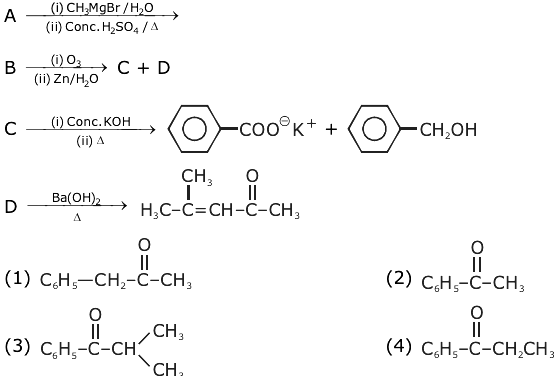
8. The major product of the following reaction:

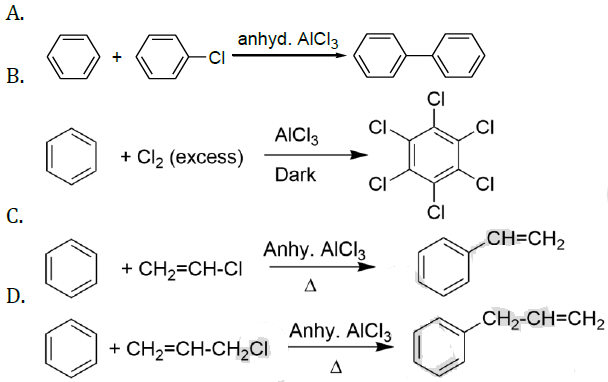
9. The correct sequence of reagents used in the preparation of 4-bromo-2-nitroethyl benzene from benzene is:
(a) CH3COCl/AlCl3, Br2/AlBr3, HNO3/H2SO4, Zn/HCl
(b) CH3COCl/AlCl3, Zn-Hg/HCl, Br2/AlBr3, HNO3/H2SO4
(c) Br2/AlBr3, CH3COCl/AlCl3, HNO3/H2SO4, Zn/HCl
(d) HNO3/H2SO4, Br2/AlCl3, CH3COCl/AlCl3, Zn-Hg/HCl
10. The major components of German Silver are:
(a) Cu, Zn and Mg
(b) Ge, Cu and Ag
(c) Zn, Ni and Ag
(d) Cu, Zn and Ni
11. The method used for the purification of Indium is:
(a) Van Arkel method
(b) Vapour phase refining
(c) Zone refining
(d) Liquation
12. Which of the following is correct structure of α-anomer of maltose

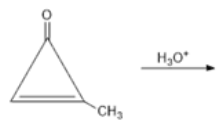
13. The major product of the following reaction is:
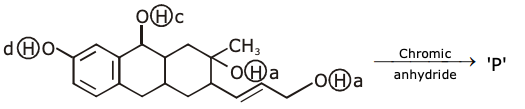
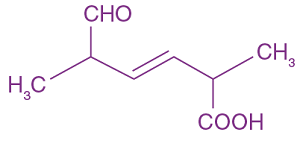
![]()
(a) CH3CH2CH2CHO
(b) CH3CH2CH=CH―CHO
(c) CH3CH2CH2CH2CHO
(d) 
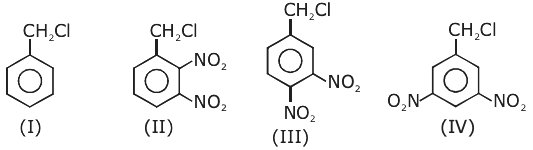
14. The correct order of acid character of the following compounds is:

(a) II > III > IV > I
(b) III > II > I > IV
(c) IV > III > II > I
(d) I > II > III > IV
15. Which among the following species has unequal bond lengths?
(a) XeF4
(b) SiF4
(c) BF4−
(d) SF4
16. Given below are two statements:
Statement I: α and β forms of sulphur can change reversibly between themselves with slow heating or slow cooling.
Statement II: At room temperature the stable crystalline form of sulphur is monoclinic sulphur.
In the light of the above statements, choose the correct answer from the options given below.
(a) Both statement I and statement II are false
(b) Statement I is true but statement II is false
(c) Both statement I and statement II are true
(d) Statement I is false but statement II is true
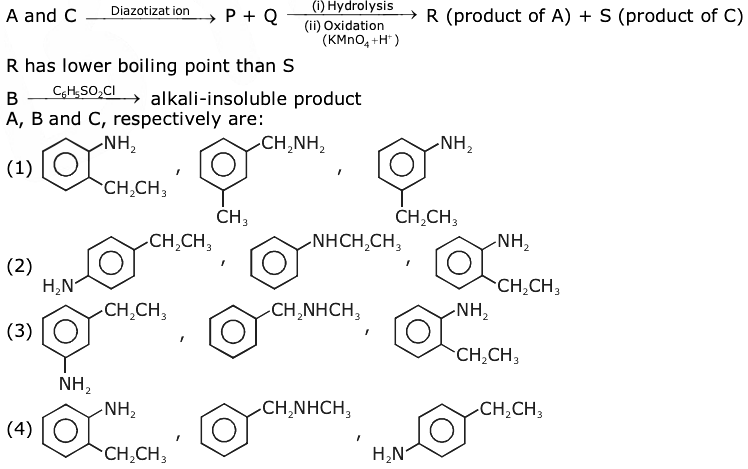
17. Correct statement about the given chemical reaction is:

(a) Reaction is possible and compound (A) will be a major product.
(b) The reaction will form a sulphonated product instead of nitration.
(c) NH2 group is ortho and para directive, so product (B) is not possible.
(d) Reaction is possible and compound (B) will be the major product.
18. Which of the following compound is added to the sodium extract before addition of silver nitrate for testing of halogens?
(a) Nitric acid
(b) Sodium hydroxide
(c) Hydrochloric acid
(d) Ammonia
19. Given below are two statements:
Statement I: The pH of rain water is normally ~5.6.
Statement II: If the pH of rain water drops below 5.6, it is called acid rain.
In the light of the above statements, choose the correct answer from the option given below.
(a) Statement I is false but Statement II is true
(b) Both statement I and statement II are true
(c) Both statement I and statement II are false
(d) Statement I is true but statement II is false
20. The solubility of Ca(OH)2 in water is:
[Given: The solubility product of Ca(OH)2 in water = 5.5 × 10−6]
(a) 1.1 × 10−6
(b) 1.77 × 10−6
(c) 1.7 × 10−2
(d) 1.11 × 10−2
Section-B
21. If a compound AB dissociates to the extent of 75% in an aqueous solution, the molality of the solution which shows a 2.5 K rise in the boiling point of the solution is ______molal.
22. The spin only magnetic moment of a divalent ion in aqueous solution (atomic number 29) is ____BM.
23. The number of compound/s given below which contain/s —COOH group is ______
(a) Sulphanilic acid
(b) Picric acid
(c) Aspirin
(d) Ascorbic acid
24. The unit cell of copper corresponds to a face centered cube of edge length 3.596 Å with one copper atom at each lattice point. The calculated density of copper in kg/m3 is ______.
25. Consider titration of NaOH solution versus 1.25 M oxalic acid solution. At the end point following burette readings were obtained.
(i) 4.5 mL (ii) 4.5 mL (iii) 4.4 mL (iv) 4.4 mL (v) 4.4 mL
If the volume of oxalic acid taken was 10.0 ml. then the molarity of the NaOH solution is ____M. (Rounded-off to the nearest integer)
26. Electromagnetic radiation of wavelength 663 nm is just sufficient to ionize the atom of metal A. The ionization energy of metal A in kJ mol−1 (Rounded off to the nearest integer)
[h=6.63 × 10−34Js, c = 3.00 × 108 ms−1, NA=6.02 × 1023 mol−1]
27. The rate constant of a reaction increases by five times on increasing temperature from 27°C to 52° The value of activation energy in kJ mol−1 is ______.
(Rounded off to the nearest integer)
[R=8.314 J K−1 mol−1]
28. Copper reduces into NO and NO2 depending upon the concentration of HNO3 in solution. (Assuming fixed [Cu2+] and PNO = PNO2), the HNO3 concentration at which the thermodynamic tendency for reduction of into NO and NO2 by copper is same is 10x
The value of 2x is ______. (Rounded-off to the nearest integer)
[Given ![]()
![]() and at 298 K,
and at 298 K, ![]() ]
]
29. Five moles of an ideal gas at 293 K is expanded isothermally from an initial pressure of 2.1 MPa to 1.3 MPa against a constant external 4.3 MPa. The heat transferred in this process is ____kJ mol−1. (Rounded-off of the nearest integer)
[Use R = 8.314 J mol−1 K−1]
30. Among the following, the number of metal/s which can be used as electrodes in the photoelectric cell is _____(Integer answer).
(a) Li
(b) Na
(c) Rb
(d) Cs
Mathematics
Section-A
1. A plane passes through the points A(1,2,3), B(2,3,1) and C(2,4,2). If O is the origin and P is (2,–1,1), then the projection of vector ![]() on this plane is of length:
on this plane is of length:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
2. The contrapositive of the statement “If you will work, you will earn money” is:
(a) If you will not earn money, you will not work
(b) You will earn money, if you will not work
(c) If you will earn money, you will work
(d) To earn money, you need to work
3. If α, β∈ R are such that 1 – 2i (here i2 = –1) is a root of z2 + αz + β = 0, then (α – β) is equal to:
(a) 7
(b) −3
(c) 3
(d) −7
4. If ![]() then
then
(a) ![]()
(b) ![]()
(c) I2 + I4, I3 + I5, I4 + I6 are in A.P.
(d) I2 + I4, I3 + I5, I4 + I6 are in G.P.
5. If for the matrix,  AAT = I2, then t he value of α4 + β4 is:
AAT = I2, then t he value of α4 + β4 is:
(a) 1
(b) 3
(c) 2
(d) 4
6. Let x denote the total number of one-one functions from a set A with 3 elements to a set B with 5 elements and y denote the total number of one-one functions from the set A to the set A × B. Then:
(a) y = 273x
(b) 2y = 91x
(c) y = 91x
(d) 2y = 273x
7. If the curve x2 + 2y2 = 2 intersects the line x + y = 1 at two points P and Q, then the angle subtended by the line segment PQ at the origin is:
(a) 
(b) 
(c) 
(d) 
8. The integral  is equal to:
is equal to:
(where c is a constant of integration)
(a) loge|x2 + 5x – 7| +c
(b) ![]()
(c) 4loge|x2 + 5x – 7| + c
(d) ![]()
9. A hyperbola passes through the foci of the ellipse ![]() and its transverse and conjugate axes coincide with major and minor axes of the ellipse, respectively. If the product of their eccentricities is one, then the equation of the hyperbola is:
and its transverse and conjugate axes coincide with major and minor axes of the ellipse, respectively. If the product of their eccentricities is one, then the equation of the hyperbola is:
(a) ![]()
(b) ![]()
(c) x2 – y2 = 9
(d) ![]()
10.  is equal to:
is equal to:
(a) 1
(b) 1/3
(c) 1/2
(d) 1/4
11. In a group of 400 people, 160 are smokers and non-vegetarian; 100 are smokers and vegetarian and the remaining 140 are non-smokers and vegetarian. Their chances of getting a particular chest disorder are 35%, 20% and 10% respectively. A person is chosen from the group at random and is found to be suffering from chest disorder. The probability that the selected person is a smoker and non-vegetarian is:
(a) 7/45
(b) 8/45
(c) 14/45
(d) 28/45
12. The following system of linear equations
2x + 3y + 2z = 9
3x + 2y + 2z = 9
x – y + 4z = 8
(a) does not have any solution
(b) has a unique solution
(c) has a solution (α, β, γ) satisfying α + β2 + γ3 = 12
(d) has infinitely many solutions
13. The minimum value of ![]() where a, x ∈ R and a > 0, is equal to:
where a, x ∈ R and a > 0, is equal to:
(a) ![]()
(b) a + 1
(c) 2a
(d) 2√a
14. A function f(x) is given by  then the sum of the series
then the sum of the series ![]() is equal to:
is equal to:
(a) 19/2
(b) 49/2
(c) 39/2
(d) 29/2
15. Let α and β be the roots of x2 – 6x – 2 = 0. If an = αn – βn for n ≥ 1, then the value of  is:
is:
(a) 4
(b) 1
(c) 2
(d) 3
16. Let A be a 3 × 3 matrix with det(A) = 4. Let Ri denote the ith row of A. If a matrix B is obtained by performing the operation R2→ 2R2 + 5R3 on 2A, then det(B) is equal to:
(a) 64
(b) 16
(c) 80
(d) 128
17. The shortest distance between the line x – y = 1 and the curve x2 = 2y is:
(a) 1/2
(b) 0
(c) 1/2√2
(d) 1/√2
18. Let A be a set of all 4-digit natural numbers whose exactly one digit is 7. Then the probability that a randomly chosen element of A leaves remainder 2 when divided by 5 is:
(a) 1/5
(b) 2/9
(c) 97/297
(d) 122/297
19.  is equal to:
is equal to:
(a) 75/56
(b) 65/56
(c) 56/33
(d) 65/33
20. If 0 < x, y < π and cos x + cos y – cos (x + y) = 3/2, then sin x + cos y is equal to:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
Section-B
21. If  exists and is equal to b, then the value of a – 2b is _________.
exists and is equal to b, then the value of a – 2b is _________.
22. A line is a common tangent to the circle (x – 3)2 + y2 = 9 and the parabola y2 = 4x. If the two points of contact (a, b) and (c, d) are distinct and lie in the first quadrant, then 2(a+c) is equal to ______.
23. The value of ![]() is ______.
is ______.
24. If the remainder when x is divided by 4 is 3, then the remainder when (2020 + x)2022 is divided by 8 is ______.
25. A line L passing through origin is perpendicular to the lines
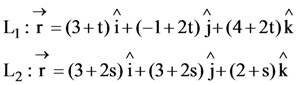
If the co-ordinates of the point in the first octant on L2 at the distance of √17 from the point of intersection of L and L1 are (a, b, c), then 18(a + b + c) is equal to ______.
26. A function f is defined on [–3, 3] as

where [x] denotes the greatest integer ≤ x. The number of points, where f is not differentiable in (–3, 3) is ______.
27. If the curves x = y4 and xy = k cut at right angles, then (4k)6 is equal to ______.
28. The total number of two digit numbers ‘n’, such that 3n + 7n is a multiple of 10, is ______.
29. Let ![]() If the area of the parallelogram whose adjacent sides are represented by the vectors
If the area of the parallelogram whose adjacent sides are represented by the vectors ![]() is 8√3 square units, then
is 8√3 square units, then ![]() is equal to________.
is equal to________.
30. If the curve y = y(x) represented by the solution of the differential equation (2xy2 – y)dx + xdy = 0, passes through the intersection of the lines, 2x – 3y = 1 and 3x + 2y = 8, then |y(1)| is equal to ______.








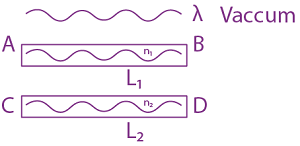
 will be:
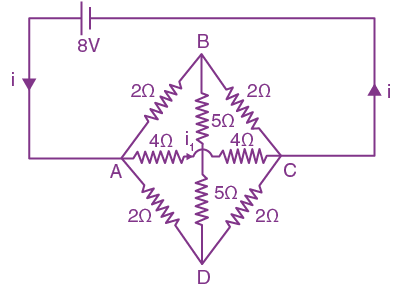
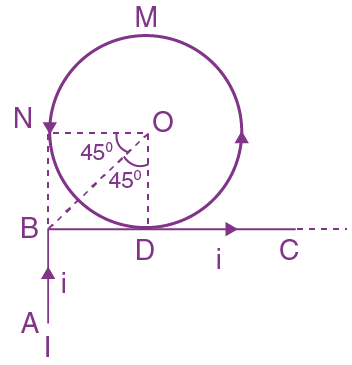
will be: The ratio of flux of reported field through the rectangular surface of area 0.2 m2 (parallel to y-z plane) to that of the surface of area 0.3 m2 (parallel to x-z plane) is a : 2, where a = ________
The ratio of flux of reported field through the rectangular surface of area 0.2 m2 (parallel to y-z plane) to that of the surface of area 0.3 m2 (parallel to x-z plane) is a : 2, where a = ________










 is
is



 then:
then: is equal to:
is equal to: then this curve also passes through the point :
then this curve also passes through the point : where [t] denotes the greatest integer ≤ t, is :
where [t] denotes the greatest integer ≤ t, is : and
and  then 13(a2 + b2) is equal to ________.
then 13(a2 + b2) is equal to ________. where x, y and z are real numbers such that x + y + z > 0 and xyz = 2.
where x, y and z are real numbers such that x + y + z > 0 and xyz = 2.




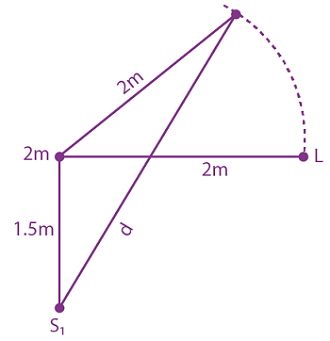
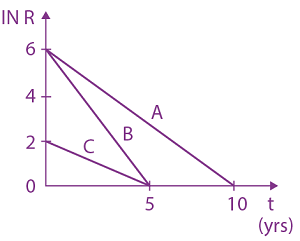
 Measured value of ‘L’ is 1.0 m from meter-scale having a minimum division of 1 mm and time of one complete oscillation is 1.95 s measured from stopwatch of 0.01 s resolution. The percentage error in the determination of ‘g’ will be:
Measured value of ‘L’ is 1.0 m from meter-scale having a minimum division of 1 mm and time of one complete oscillation is 1.95 s measured from stopwatch of 0.01 s resolution. The percentage error in the determination of ‘g’ will be:














 The value of x will be __________.
The value of x will be __________.








 is (20, b, −a, −9), then |a + b| is equal to:
is (20, b, −a, −9), then |a + b| is equal to: for all x ∈ R, then the value of f(1) lies in the interval:
for all x ∈ R, then the value of f(1) lies in the interval: is :
is :

 is________.
is________. and n = [|k|] be the greatest integral part of |k|. Then
and n = [|k|] be the greatest integral part of |k|. Then  is equal to ________.
is equal to ________.












 where x is the displacement, k is the Boltzmann constant and T is the temperature. α and β are constants. Then the dimensions of β will be:
where x is the displacement, k is the Boltzmann constant and T is the temperature. α and β are constants. Then the dimensions of β will be:
























 where [.] denotes the greatest integer function, then f is:
where [.] denotes the greatest integer function, then f is: is equal to:
is equal to: where c is a constant o integration, then the ordered pair (a, b) is equal to:
where c is a constant o integration, then the ordered pair (a, b) is equal to: is:
is: where α ∈ ℝ. Suppose Q = [qij] is a matrix satisfying PQ = kI3 for some non-zero k ∈ ℝ. If q23 = −k/8 and |Q| = k2/2, then a2 + k2 is equal to________
where α ∈ ℝ. Suppose Q = [qij] is a matrix satisfying PQ = kI3 for some non-zero k ∈ ℝ. If q23 = −k/8 and |Q| = k2/2, then a2 + k2 is equal to________ is equal to______
is equal to______ then the value of is_______
then the value of is_______








 where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicular to the rod is:
where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicular to the rod is:























 is the solution of the differential equation,
is the solution of the differential equation,  If B = A + A4, then det (B):
If B = A + A4, then det (B): is 405, then |k| equals:
is 405, then |k| equals: then n is equal to ………..
then n is equal to ………..



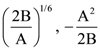
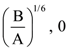
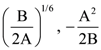

 are given, respectively by:
are given, respectively by:
 The rms electric field, in units of V/m associated with this source is close to the nearest integer is __________. (∈0 = 8.86 × 10–12 C2Nm–2; c = 3 × 108 ms–1)
The rms electric field, in units of V/m associated with this source is close to the nearest integer is __________. (∈0 = 8.86 × 10–12 C2Nm–2; c = 3 × 108 ms–1)


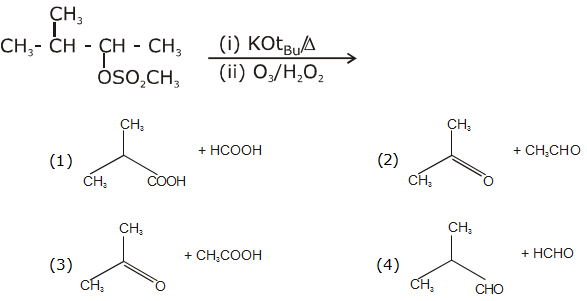

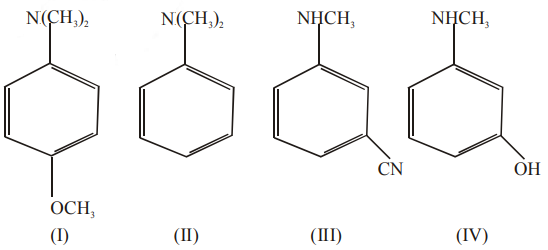
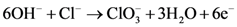
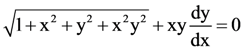 is:
is: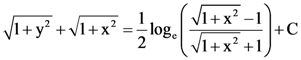

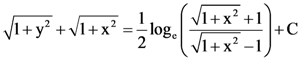
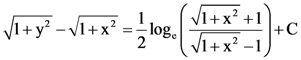
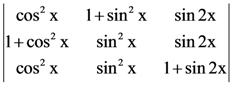
 where N is the set of all natural number, then the value of
where N is the set of all natural number, then the value of 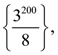 is equal to:
is equal to: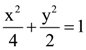 from any of its foci?
from any of its foci?
 (n, a > 1) then the standard deviation of n observations x1, x2, x3…xn is:
(n, a > 1) then the standard deviation of n observations x1, x2, x3…xn is: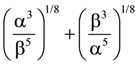 is :
is :
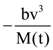
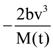
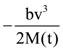
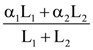
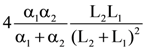
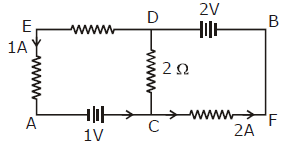

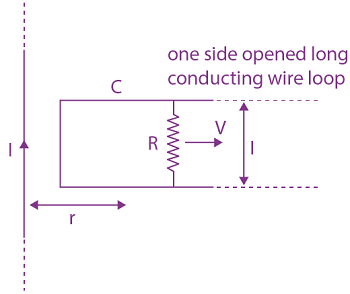
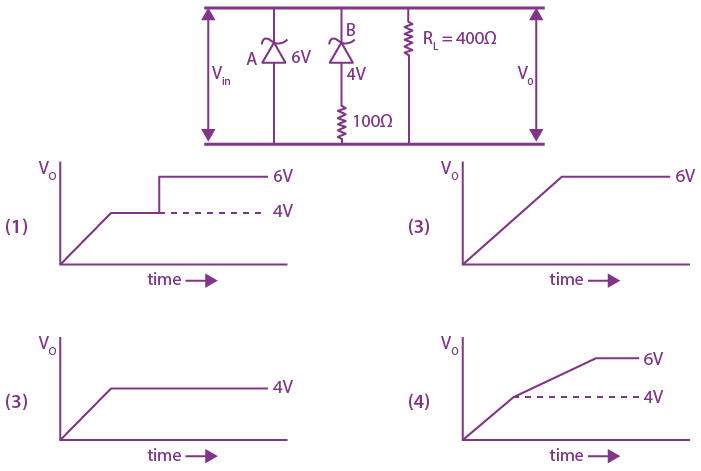
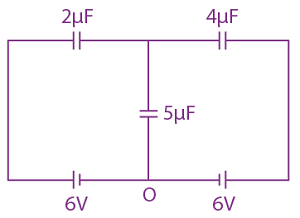
 are defined where C – capacitance, R – Resistance, L – length, E – Electric field, B – magnetic field and ε0, μ0 – free space permittivity and permeability respectively. Then:
are defined where C – capacitance, R – Resistance, L – length, E – Electric field, B – magnetic field and ε0, μ0 – free space permittivity and permeability respectively. Then: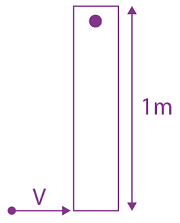
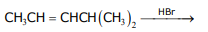
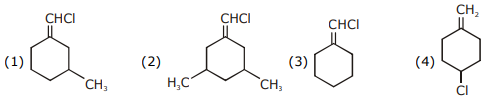
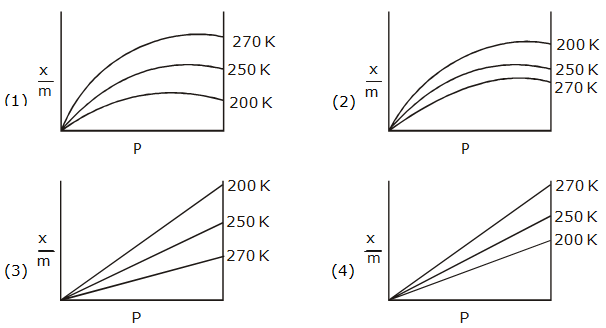
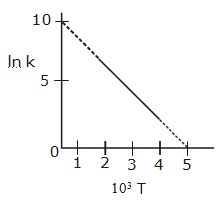
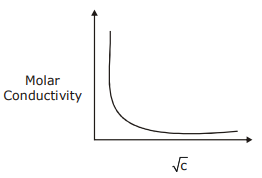

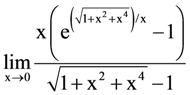
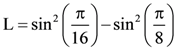 and
and 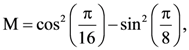 then:
then: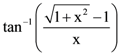 with respect to
with respect to 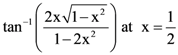 is:
is: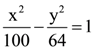 and the circle x2 + y2 = 36, then which one of the following is true?
and the circle x2 + y2 = 36, then which one of the following is true?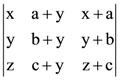 is equal to:
is equal to: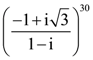 is:
is: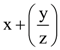 is equal to:
is equal to: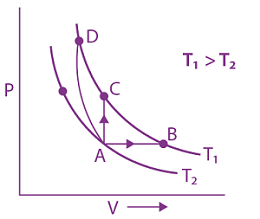
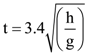

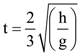
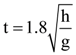
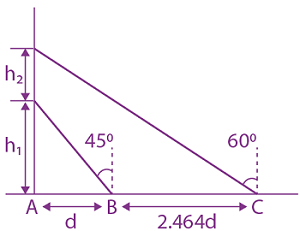
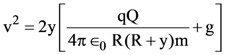
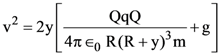
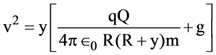
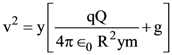
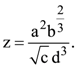 The percentages of error in the measurement of a, b, c and d are 2% , 1.5%, 4% and 2.5% respectively. The percentage of error in z is :
The percentages of error in the measurement of a, b, c and d are 2% , 1.5%, 4% and 2.5% respectively. The percentage of error in z is :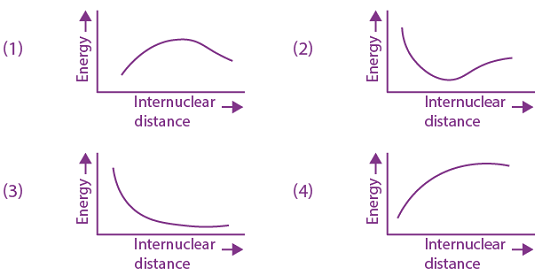



 are m and M respectively, then the ordered pair (m, M) is equal to:
are m and M respectively, then the ordered pair (m, M) is equal to: satisfying y(0) = 1, then the value of y(loge 13) is:
satisfying y(0) = 1, then the value of y(loge 13) is: is:
is: is twice differentiable, then the ordered pair (k1, k2) is equal to:
is twice differentiable, then the ordered pair (k1, k2) is equal to: is equal to :
is equal to : 1540 is………….
1540 is………….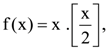 for −10 < x < 10, where [t] denotes the greatest integer function. Then the number of points of discontinuity of f is equal to………….
for −10 < x < 10, where [t] denotes the greatest integer function. Then the number of points of discontinuity of f is equal to………….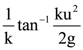
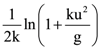
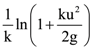


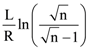
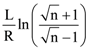




 then the determinant of A is equal to
then the determinant of A is equal to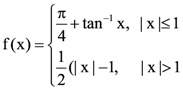 is:
is: where each Xi contains 10 elements and each Yi contains 5 elements. If each element of the set T is an element of exactly 20 of sets Xi ’s and exactly 6 of sets Yi’s, then n is equal to :
where each Xi contains 10 elements and each Yi contains 5 elements. If each element of the set T is an element of exactly 20 of sets Xi ’s and exactly 6 of sets Yi’s, then n is equal to : is equal to ______
is equal to ______ in the x-direction. The magnitude of gravitational potential on the x-axis at a distance x, taking its value to be zero at infinity, is:
in the x-direction. The magnitude of gravitational potential on the x-axis at a distance x, taking its value to be zero at infinity, is:
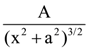
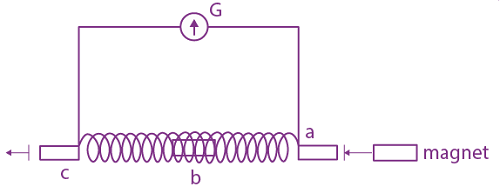
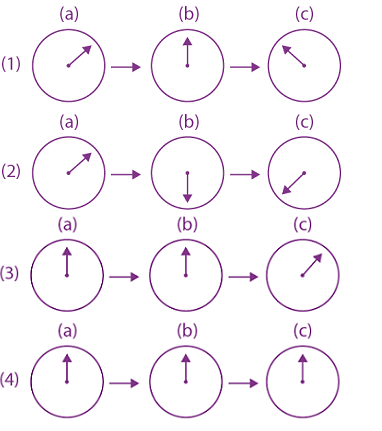



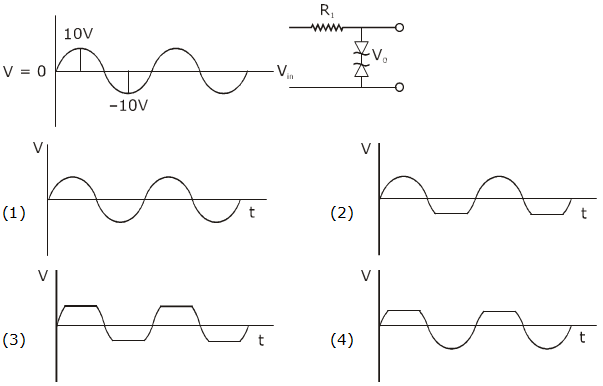



 is equal to
is equal to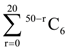 is equal to:
is equal to: If the normal to it at P intersects the x-axis at (9, 0) and e is its eccentricity, then the ordered pair (a2, e2) is equal to:
If the normal to it at P intersects the x-axis at (9, 0) and e is its eccentricity, then the ordered pair (a2, e2) is equal to: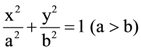 be a given ellipse, length of whose latus rectum is 10. If its eccentricity is the maximum value of the function,
be a given ellipse, length of whose latus rectum is 10. If its eccentricity is the maximum value of the function, 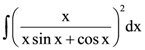 is equal to
is equal to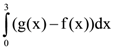 is equal to:
is equal to: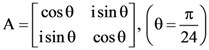 and
and 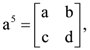 where i = √−1 then which one of the following is not true?
where i = √−1 then which one of the following is not true?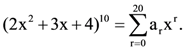 Then a7/a13 is equal to………..
Then a7/a13 is equal to………..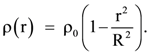 Then the gravitational field is maximum at:
Then the gravitational field is maximum at: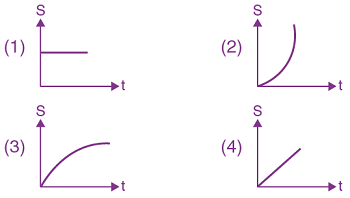

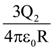
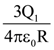

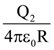
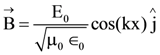
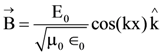
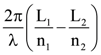
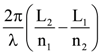
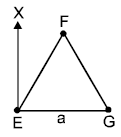



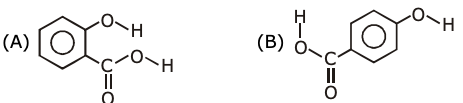

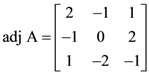 and B = adj(adj A). If |A| = λ and |(B−1)T|=μ, then the ordered pair, (|λ|, μ) is equal to:
and B = adj(adj A). If |A| = λ and |(B−1)T|=μ, then the ordered pair, (|λ|, μ) is equal to: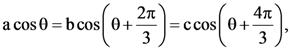 where θ = π/9, then the angle between the vectors
where θ = π/9, then the angle between the vectors 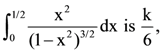 then k is equal to:
then k is equal to: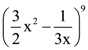 is k, then 18 k is equal to:
is k, then 18 k is equal to: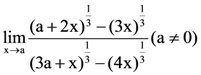 is equal to:
is equal to: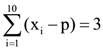 and
and 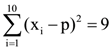 where 0 ≠ p ε R , then the standard deviation of these observations is :
where 0 ≠ p ε R , then the standard deviation of these observations is :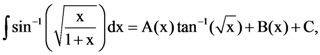 where C is a constant of integration, then the ordered pair (A(x), B(x)) can be:
where C is a constant of integration, then the ordered pair (A(x), B(x)) can be: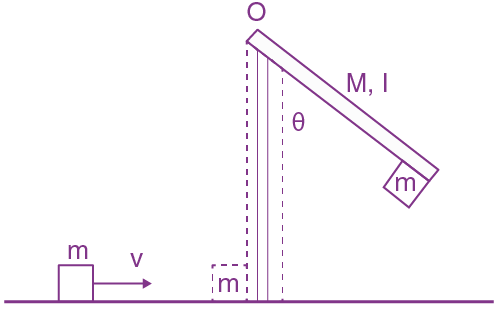
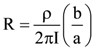


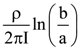
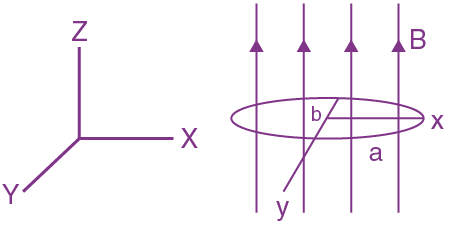
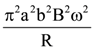
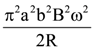
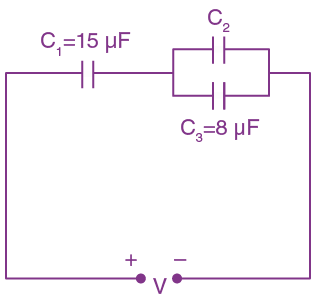

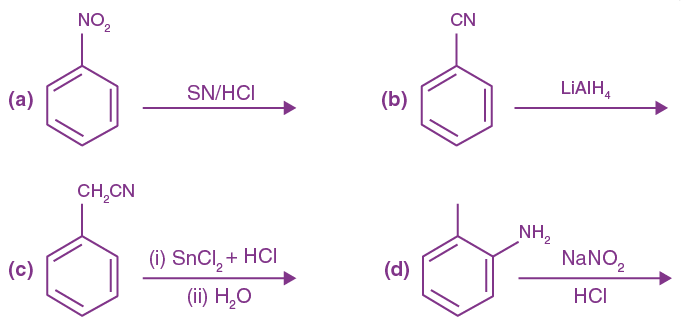

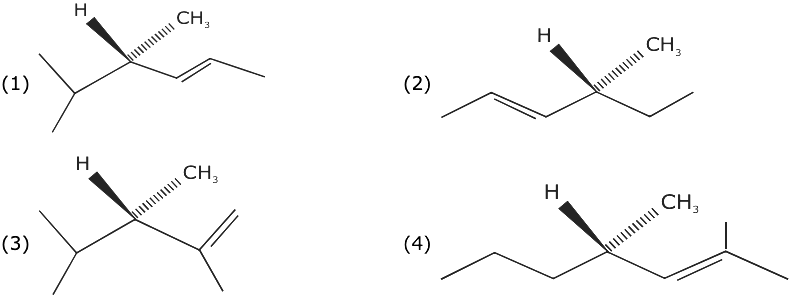
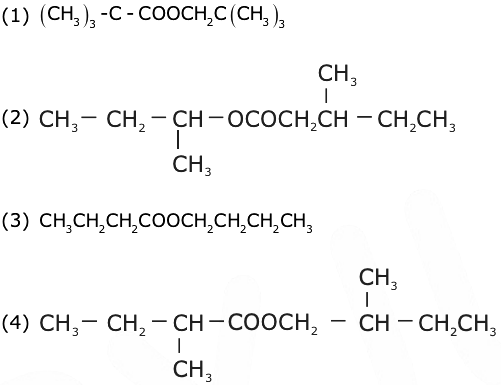
 = AX3 + BX2 + Cx + D, then B + C is equal to:
= AX3 + BX2 + Cx + D, then B + C is equal to: is equal to:
is equal to:
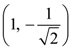
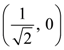
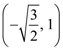
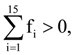 the standard deviation cannot be:
the standard deviation cannot be: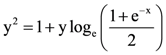
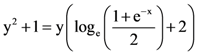
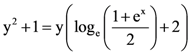
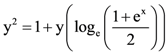
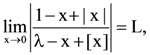 then L is equal to:
then L is equal to: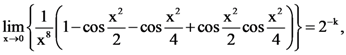 then the value of k is …….
then the value of k is …….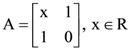 and A4[aij]. If a11 = 109, then a22 is equal to…………….
and A4[aij]. If a11 = 109, then a22 is equal to…………….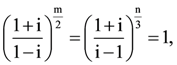 (m, n ∈ N) then the greatest common divisor of the least values of m and n is……………..
(m, n ∈ N) then the greatest common divisor of the least values of m and n is……………..






















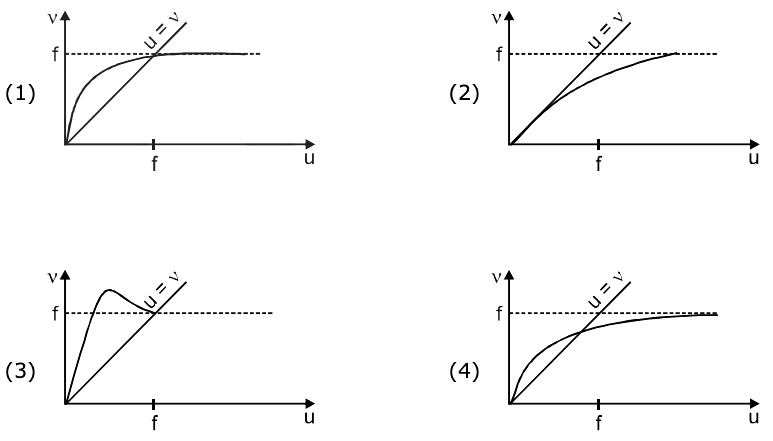
 then the value of n, for which g(n) = 20, is:
then the value of n, for which g(n) = 20, is: then the set A:
then the set A: then k is equal to:
then k is equal to:
 is equal to :
is equal to : ATA = I, then a value of abc can be:
ATA = I, then a value of abc can be: then λ is equal to_______
then λ is equal to_______ then (dy/dx) at x = 0 is:
then (dy/dx) at x = 0 is: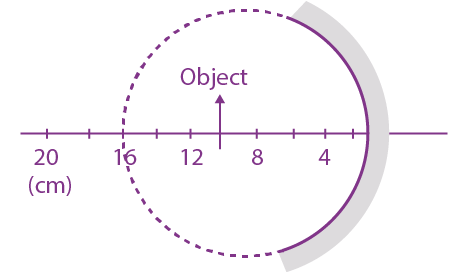


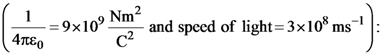

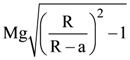



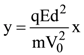
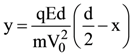
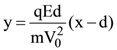
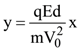

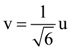
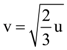

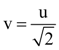
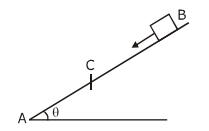




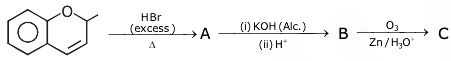

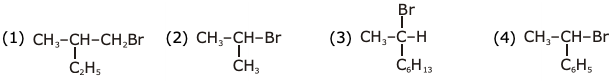
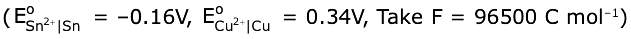
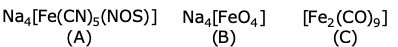
 is (−∞, −a] ∪ [a, ∞). Then a is equal to :
is (−∞, −a] ∪ [a, ∞). Then a is equal to : be continuous for some a, b, c ∈ R and f´(0) + f´(2) = e, then the value of a is:
be continuous for some a, b, c ∈ R and f´(0) + f´(2) = e, then the value of a is:
 is :
is :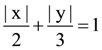 and inside the ellipse
and inside the ellipse  is:
is: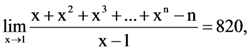 (n ∈ N) then the value of n is equal to:
(n ∈ N) then the value of n is equal to: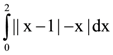 is equal to:
is equal to: and carries a current i. The electron gun shoots an electron along the radius of solenoid with speed If the electron does not hit the surface of the solenoid, maximum possible value of v is (all symbols have their standard meaning):
and carries a current i. The electron gun shoots an electron along the radius of solenoid with speed If the electron does not hit the surface of the solenoid, maximum possible value of v is (all symbols have their standard meaning):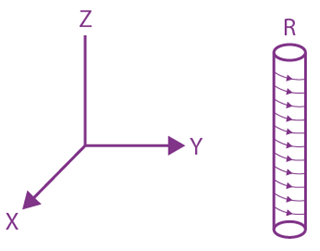


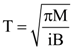
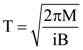
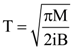
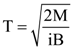
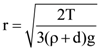
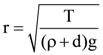

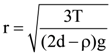
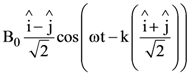
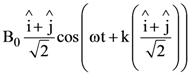

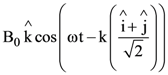
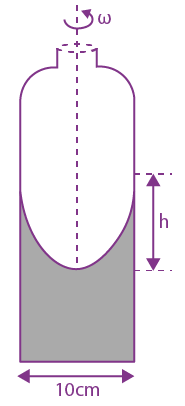
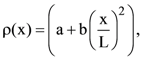 where a and b are constants and 0 ≤ x ≤ The value of x for the center of mass of the rod is at:
where a and b are constants and 0 ≤ x ≤ The value of x for the center of mass of the rod is at:


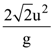
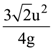

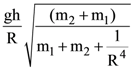


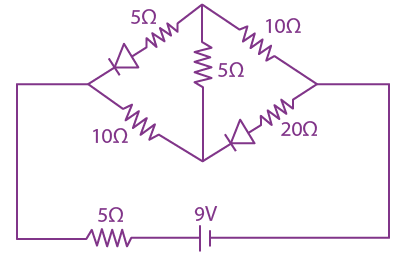







 if l1 is the least value of the term independent of x when
if l1 is the least value of the term independent of x when 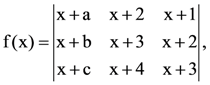 then:
then: and
and  Then the area (in sq. units) of the region bounded by the curves y = f(x) and y = g(x) between the lines 2x = 1 to 2x = √3 is:
Then the area (in sq. units) of the region bounded by the curves y = f(x) and y = g(x) between the lines 2x = 1 to 2x = √3 is:
 then a value of x satisfying y(x) = e is:
then a value of x satisfying y(x) = e is: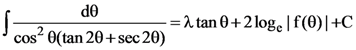 where C is constant if integration, then the ordered pair (λ, f(θ)) is equal to:
where C is constant if integration, then the ordered pair (λ, f(θ)) is equal to: then k is equal to ________.
then k is equal to ________.
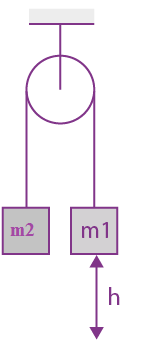
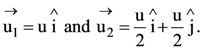 They collide completely inelastically. Find the loss in kinetic energy.
They collide completely inelastically. Find the loss in kinetic energy.
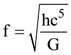 , where c is speed of light, G is universal gravitational constant and h is the Planck’s constant. Dimension of f is that of;
, where c is speed of light, G is universal gravitational constant and h is the Planck’s constant. Dimension of f is that of;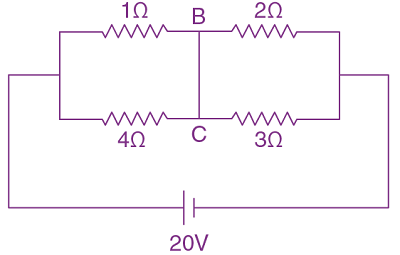
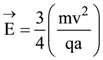
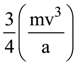

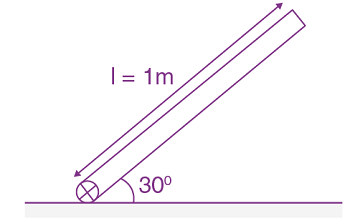
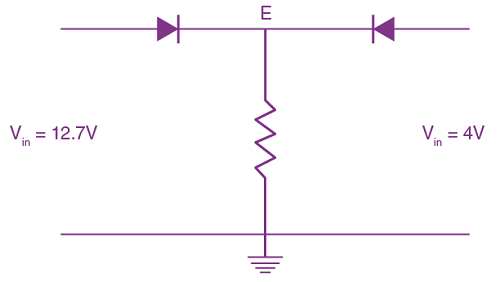

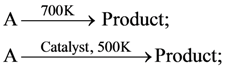
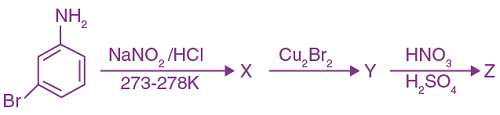
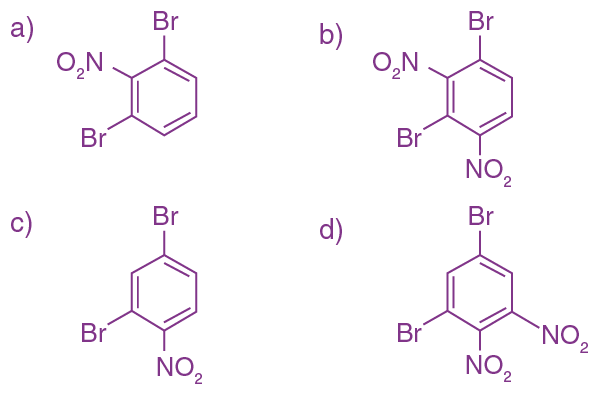
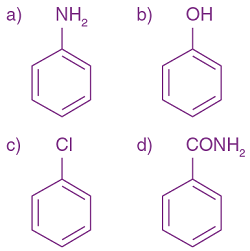
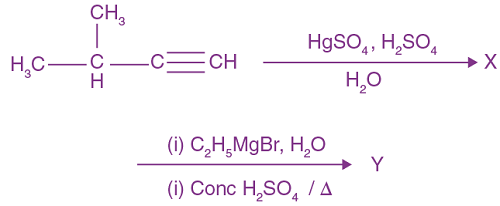
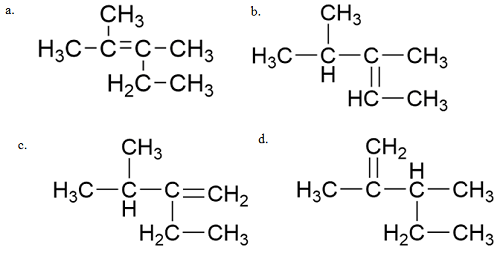

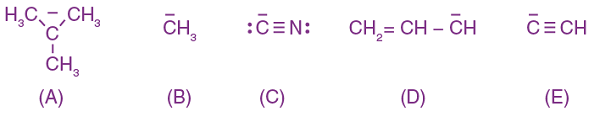
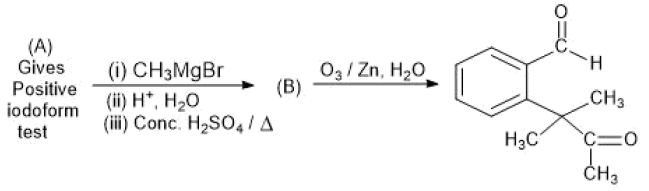
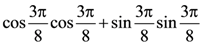 is:
is: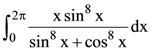 is equal to:
is equal to: and the hyperbola,
and the hyperbola, 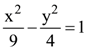 respectively and (e1, e2) is a point on the ellipse, 15x2 + 3y2 = k. Then k is equal to:
respectively and (e1, e2) is a point on the ellipse, 15x2 + 3y2 = k. Then k is equal to: is continuous at x = 0 then a + 2b is equal to:
is continuous at x = 0 then a + 2b is equal to: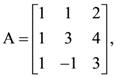 B = adj A and C = 3A, then
B = adj A and C = 3A, then 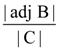 is equal to:
is equal to: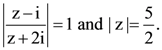 Then the value of |z + 3i| is:
Then the value of |z + 3i| is: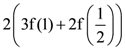
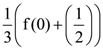
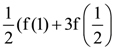
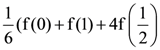
 is equal to: (where C is a constant of integration)
is equal to: (where C is a constant of integration)
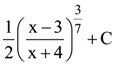
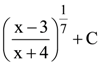
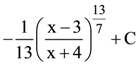
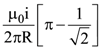

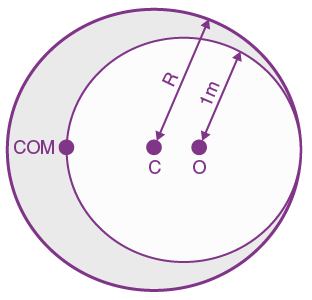
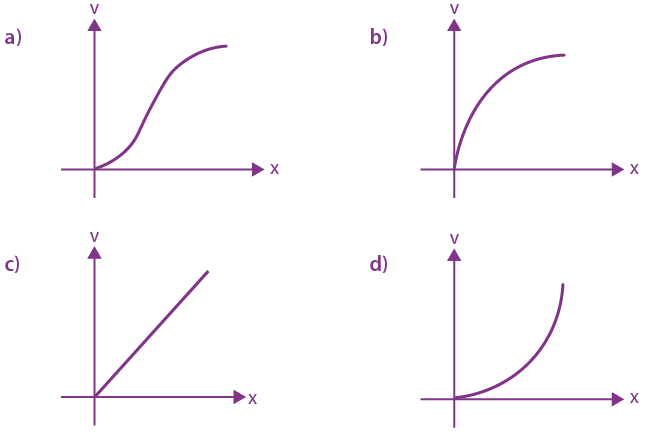
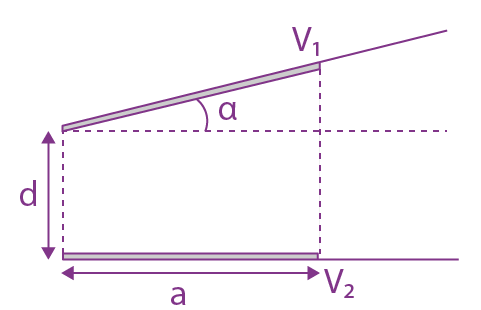
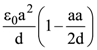
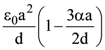

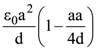
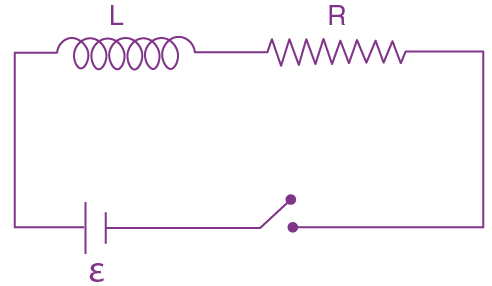
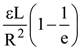
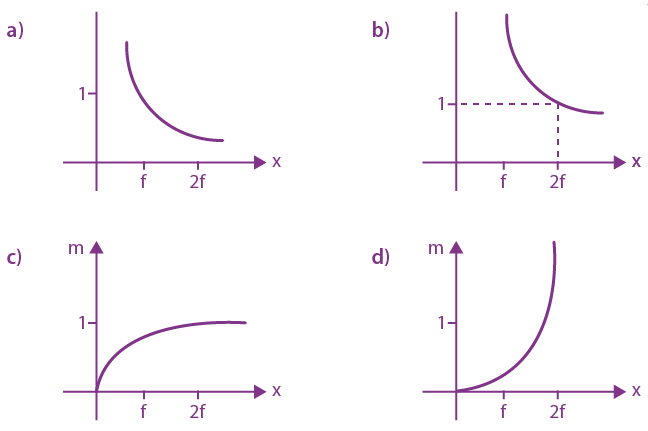
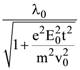
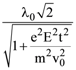
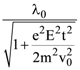
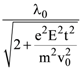

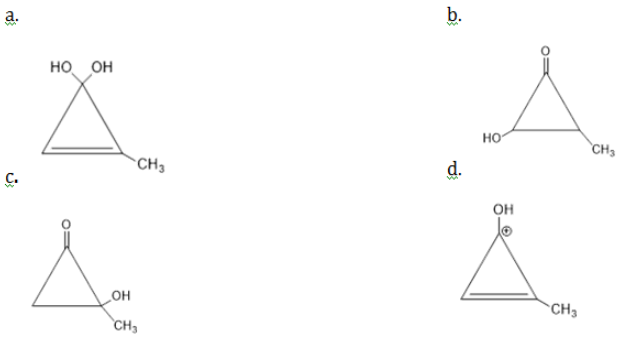


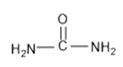
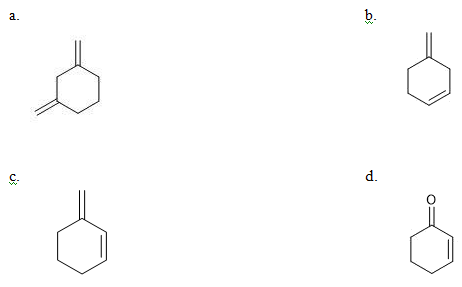
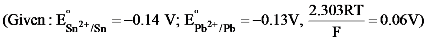
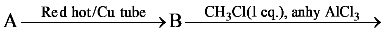
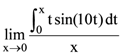 is equal to:
is equal to: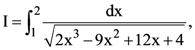 then:
then: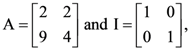 then 10A−1 is equal to:
then 10A−1 is equal to: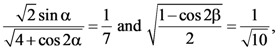
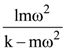
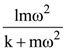

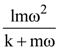
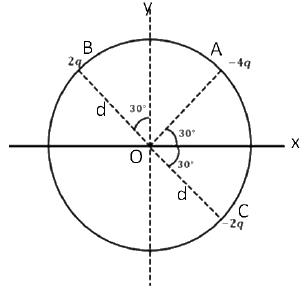



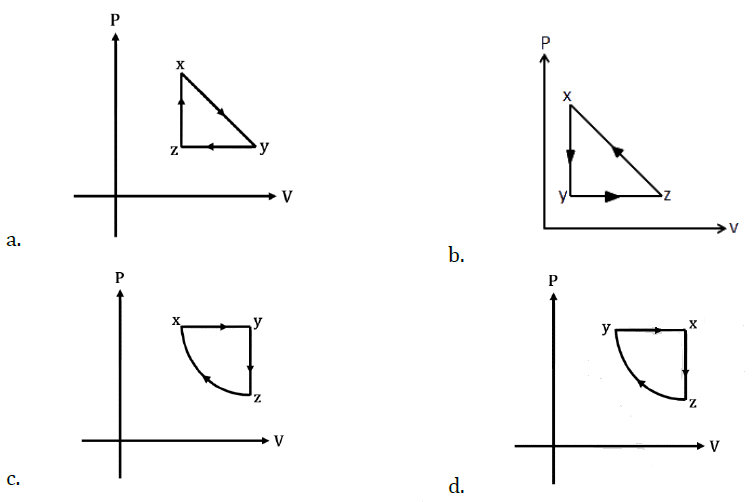



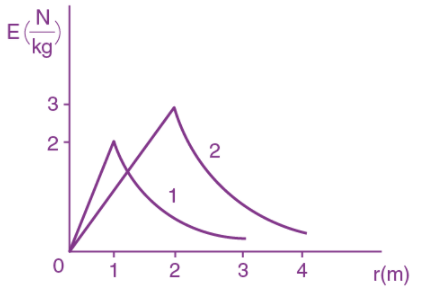
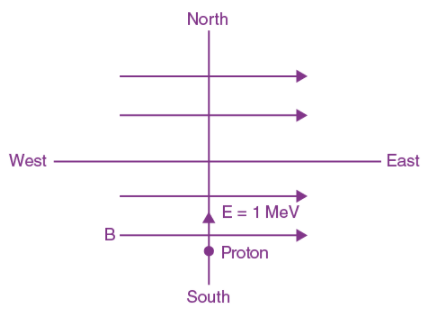
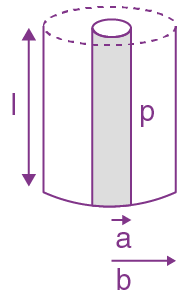
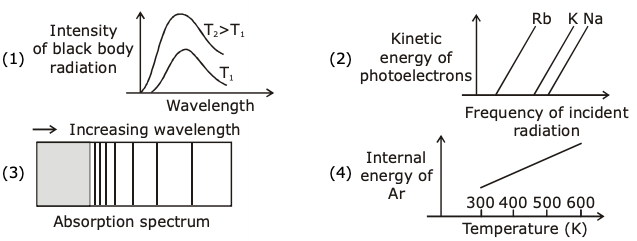
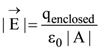 is applicable. In the formula Ɛ0 is permittivity of free space, A is area of Gaussian and qenc is charge enclosed by the Gaussian surface. This equation can be used in which of the following equation?
is applicable. In the formula Ɛ0 is permittivity of free space, A is area of Gaussian and qenc is charge enclosed by the Gaussian surface. This equation can be used in which of the following equation?
 The minimum density of a liquid in which it float is just
The minimum density of a liquid in which it float is just


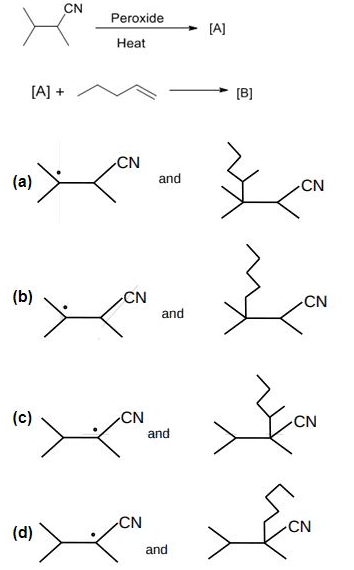
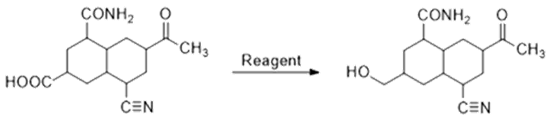
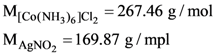
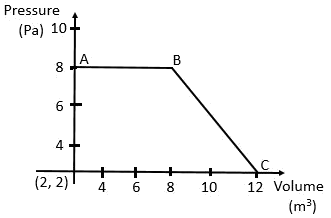
 is
is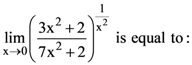
 where c is a constant of integration, then λf(π/3) is equal to :
where c is a constant of integration, then λf(π/3) is equal to :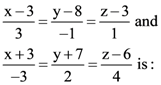
 in the interval [3, 4], where a ∈ R, then f′′(c) is equal to:
in the interval [3, 4], where a ∈ R, then f′′(c) is equal to: is given by
is given by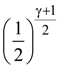
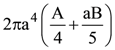

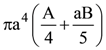
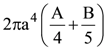

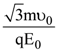
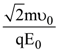
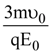
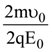
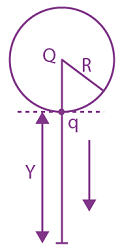
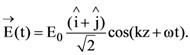 At t = 0, a positively charged particle is at the point (x, y, z) = (0, 0, π/k). If its instantaneous velocity at t = 0 is
At t = 0, a positively charged particle is at the point (x, y, z) = (0, 0, π/k). If its instantaneous velocity at t = 0 is 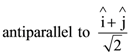


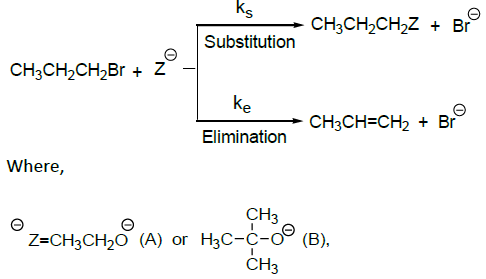
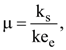 the correct option is______.
the correct option is______.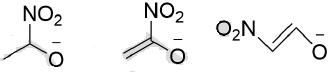

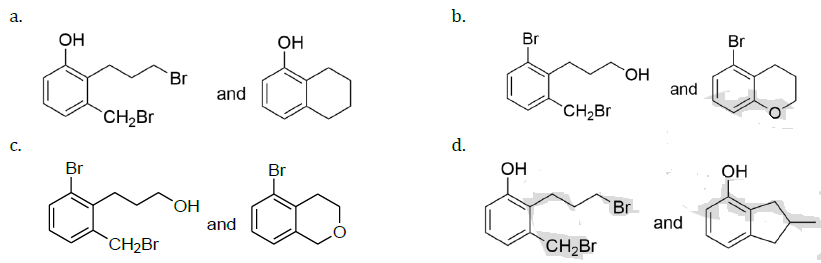
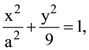 for some a ∈ R then the distance between the foci of the ellipse is:
for some a ∈ R then the distance between the foci of the ellipse is:
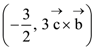
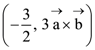

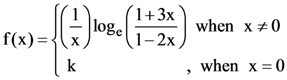


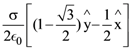
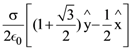

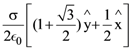

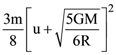
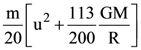
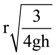


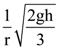




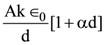
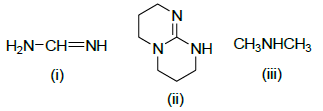
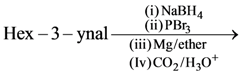




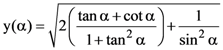 where
where  then the matrix A31 is equal to
then the matrix A31 is equal to then k is
then k is such that y(0) = 0, then y(1) is equal to
such that y(0) = 0, then y(1) is equal to