JEE Main Session 2 26th June 2022 Shift 2
PHYSICS
Section-A
IMPORTANT INSTRUCTIONS:
(1) The test is of 3 hours duration:
(2) The Test Booklet consists of 90 questions. The maximum marks are 300.
(3) There are three parts in the question paper consisting of Physics, Chemistry and Mathematics having 30 questions in each part of equal weightage. Each part (subject) has two sections.
(i) Section-A: This section contains 20 multiple choice questions which have only one correct answer. each question carries 4 marks for correct answer and −1 mark for wrong answer.
(ii) Section-B: This section contains 10 questions. In Section-B, attempt any five questions out of 10. The answer to each of the questions is a numerical value. Each question carries 4 marks for correct answer and −1 mark for wrong answer. For Section-B, the answer should be rounded off to the nearest integer.
1. The dimension of mutual inductance is :
(A) [ML2T–2A–1]
(B) [ML2T–3A–1]
(C) [ML2T–2A–2]
(D) [ML2T–3A–2]
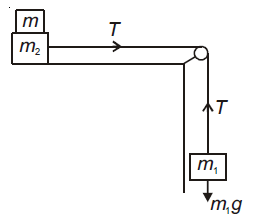
2. In the arrangement shown in figure a1, a2, a3 and a4 are the accelerations of masses m1, m2, m3 and m4 Which of the following relation is true for this arrangement?
(A) 4a1 + 2a2 + a3 + a4 = 0
(B) a1 + 4a2 + 3a3 + a4 = 0
(C) a1 + 4a2 + 3a3 + 2a4 = 0
(D) 2a1 + 2a2 + 3a3 + a4 = 0
3. Arrange the four graphs in descending order of total work done; where W1, W2, W3 and W4 are the work done corresponding to figure a, b, c and d respectively.
(A) W3> W2> W1> W4
(B) W3> W2> W4> W1
(C) W2> W3> W4> W1
(D) W2> W3> W1> W4
4. Solid spherical ball is rolling on a frictionless horizontal plane surface about its axis of symmetry. The ratio of rotational kinetic energy of the ball to its total kinetic energy is :-
(A) 2/5
(B) 2/7
(C) 1/5
(D) 7/10
5. Given below are two statements : One is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: If we move from poles to equator, the direction of acceleration due to gravity of earth always points towards the center of earth without any variation in its magnitude.
Reason R: At equator, the direction of acceleration due to the gravity is towards the center of earth. In the light of above statements, choose the correct answer from the options given below :
(A) Both A and R are true and R is the correct explanation of A.
(B) Both A and R are true but R is NOT the correct explanation of A.
(C) A is true but R is false.
(D) A is false but R is true.
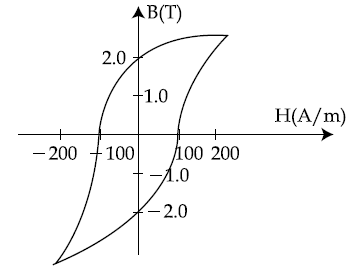
6. If ρ is the density and η is coefficient of viscosity of fluid which flows with a speed v in the pipe of diameter d, the correct formula for Reynolds number Re is:
7. A flask contains argon and oxygen in the ratio of 3:2 in mass and the mixture is kept at 27°C. The ratio of their average kinetic energy per molecule respectively will be :
(A) 3 : 2
(B) 9 : 4
(C) 2 : 3
(D) 1 : 1
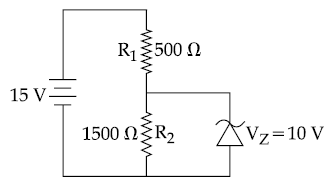
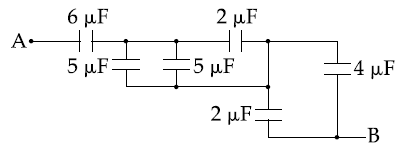
8. The charge on capacitor of capacitance 15 μF in the figure given below is
(A) 60 μc
(B) 130μc
(C) 260μc
(D) 585μc
9. A parallel plate capacitor with plate area A and plate separation d=2 m has a capacitance of 4 μ The new capacitance of the system if half of the space between them is filled with a dielectric material of dielectric constant K=3 (as shown in figure) will be :
(A) 2 μF
(B) 32μF
(C) 6μF
(D) 8μF
10. Sixty four conducting drops each of radius 0.02 m and each carrying a charge of 5 μC are combined to form a bigger drop. The ratio of surface density of bigger drop to the smaller drop will be :
(A) 1 : 4
(B) 4 : 1
(C) 1 : 8
(D) 8 : 1
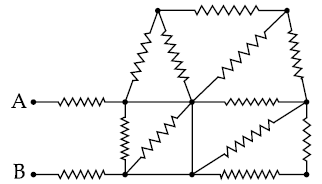
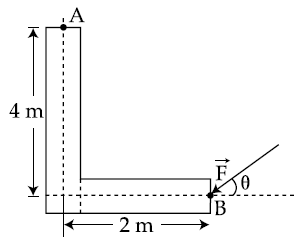
11. The equivalent resistance between points A and B in the given network is :
(A) 65 Ω
(B) 20 Ω
(C) 5 Ω
(D) 2 Ω
12. A bar magnet having a magnetic moment of 2.0 × 105 JT–1, is placed along the direction of uniform magnetic field of magnitude B= 14 × 10–5 The work done in rotating the magnet slowly through 60° from the direction of field is :
(A) 14 J
(B) 8.4 J
(C) 4 J
(D) 1.4 J
13. Two coils of self inductance L1 and L2 are connected in series combination having mutual inductance of the coils as M. The equivalent self inductance of the combination will be :
(A)
(B) L1 + L2 + M
(C) L1 + L2 + 2M
(D) L1 + L2 – 2M
14. A metallic conductor of length 1m rotates in a vertical plane parallel to east-west direction about one of its end with angular velocity 5 rad/s. If the horizontal component of earth’s magnetic field is 0.2 × 10–4 T, then emf induced between the two ends of the conductor is :
(A) 5 μV
(B) 50μV
(C) 5mV
(D) 50 mV
15. Which is the correct ascending order of wavelengths?
(A) λvisible < λX-ray < λgamma-ray < λmicrowave
(B) λgamma-ray < λX-ray < λvisible < λmicrowave
(C) λX-ray < λgamma-ra y< λvisible < λmicrowave
(D) λmicrowave < λvisible < λgamma-ray < λX-ray
16. For a specific wavelength 670 nm of light coming from a galaxy moving with velocity v, the observed wavelength is 670.7 nm.
(A) 3 × 108ms–1
(B) 3 × 1010ms–1
(C) 3.13 × 105ms–1
(D) 4.48 × 105ms–1
17. A metal surface is illuminated by a radiation of wavelength 4500 Å. The rejected photo-electron enters a constant magnetic field of 2 mT making an angle of 90° with the magnetic field. If it starts revolving in a circular path of radius 2 mm, the work function of the metal is approximately:
(A) 1.36 eV
(B) 1.69 eV
(C) 2.78 eV
(D) 2.23 eV
18. A radioactive nucleus can decay by two different processes. Half-life for the first process is 3.0 hours while it is 4.5 hours for the second process. The effective half-life of the nucleus will be:
(A) 3.75 hours
(B) 0.56 hours
(C) 0.26 hours
(D) 1.80 hours
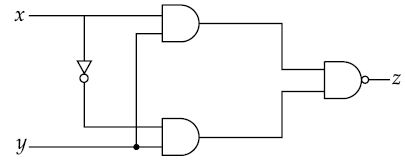
19. The positive feedback is required by an amplifier to act an oscillator. The feedback here means:
(A) External input is necessary to sustain ac signal in output
(B) A portion of the output power is returned back to the input
(C) Feedback can be achieved by LR network
(D) The base-collector junction must be forward biased
20. A sinusoidal wave y(t) = 40sin(10 × 106 πt) is amplitude modulated by another sinusoidal wave x(t) = 20sin(1000πt). The amplitude of minimum frequency component of modulated signal is:
(A) 0.5
(B) 0.25
(C) 20
(D) 10
SECTION-B
21. A ball is projected vertically upward with an initial velocity of 50 ms–1 at t = 0 s. At t = 2 s, another ball is projected vertically upward with same velocity. At t = _____s, second ball will meet the first ball.
(g = 10 ms−2)
22. A batsman hits back a ball of mass 0.4 kg straight in the direction of the bowler without changing its initial speed of 15 ms–1. The impulse imparted to the ball is _________ Ns.
23. A system to 10 balls each of mass 2 kg are connected via massless and unstretchable string. The system is allowed to slip over the edge of a smooth table as shown in figure. Tension on the string between the 7th and 8th ball is ______ N when 6th ball just leaves the table.
24. A geyser heats water flowing at a rate of 2.0 kg per minute from 30°C to 70°C. If geyser operates on a gas burner, the rate of combustion of fuel will be ____________g min–1
[Heat of combustion = 8 × 103Jg–1
Specific heat of water = 4.2 Jg–1 °C–1]
25. A heat engine operates with the cold reservoir at temperature 324 K. The minimum temperature of the hot reservoir, if the heat engine takes 300 J heat from the hot reservoir and delivers 180 J heat to the cold reservoir per cycle, is ___________K.
26. A set of 20 tuning forks is arranged in a series of increasing frequencies. If each fork gives 4 beats with respect to the preceding fork and the frequency of the last fork is twice the frequency of the first, then the frequency of last fork is _______Hz.
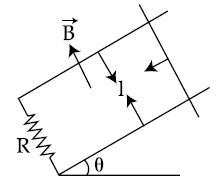
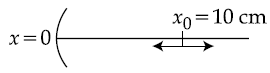
27. Two 10 cm long, straight wires, each carrying a current of 5 A are kept parallel to each other. If each wire experienced a force of 10–5 N, then separation between the wires is _____ cm.
28. A small bulb is placed at the bottom of a tank containing water to a depth of √7 m. The refractive index of water is 4/3. The area of the surface of water through which light from the bulb can emerge out is xπ m2. The value of x is ________.
29. A travelling microscope is used to determine the refractive index of a glass slab. If 40 divisions are there in 1 cm on main scale and 50 Vernier scale divisions are equal to 49 main scale divisions, then least count of the travelling microscope is _______× 10–6
30. The stopping potential for photoelectrons emitted from a surface illuminated by light of wavelength 6630 Å is 0.42 V. If the threshold frequency is x × 1013/s, where x is _________ (nearest integer).
(Given, speed of light = 3 × 108 m/s, Planck’s constant = 6.63 × 10–34Js)
CHEMISTRY
SECTION-A
1. The number of radial and angular nodes in 4d orbital are. respectively
(A) 1 and 2
(B) 3 and 2
(C) 1 and 0
(D) 2 and 1
2. Match List I with List II
Choose the most appropriate answer from the options given below :
(A) A-III, B-IV, C-II, D-I
(B) A-III, B-II, C-I, D-IV
(C) A-IV, B-III, C-I, D-II
(D) A-IV, B-II, C-III, D-I
3. Which of the following elements is considered as a metalloid?
(A) Sc
(B) Pb
(C) Bi
(D) Te
4. The role of depressants in ‘Froth Floation method’ is to
(A) Selectively prevent one component of the ore from coming to the froth
(B) Reduce the consumption of oil for froth formation
(C) Stabilize the froth
(D) Enhance non-wettability of the mineral particles.
5. Boiling of hard water is helpful in removing the temporary hardness by converting calcium hydrogen carbonate and magnesium hydrogen carbonate to
(A) CaCO3 and Mg(OH)2
(B) CaCO3 and MgCO3
(C) Ca(OH)2 and MgCO3
(D) Ca(OH)2 and Mg(OH)2
6. s-block element which cannot be qualitatively confirmed by the flame test is
(A) Li
(B) Na
(C) Rb
(D) Be
7. The oxide which contains an odd electron at the nitrogen atom is
(A) N2O
(B) NO2
(C) N2O3
(D) N2O5
8. Which one of the following is an example of disproportionation reaction?
9. The most common oxidation state of Lanthanoid elements is +3. Which of the following is likely to deviate easily from +3 oxidation state?
(A) Ce(At. No. 58)
(B) La (At. No. 57)
(C) Lu (At. No. 71)
(D) Gd(At. No. 64)
10. The measured BOD values for four different water samples (A-D) are as follows:
A = 3 ppm: B=18 ppm: C-21 ppm: D=4 ppm. The water samples which can be called as highly polluted with organic wastes, are
(A) A and B
(B) A and D
(C) B and C
(D) B and D
11. The correct order of nucleophilicity is
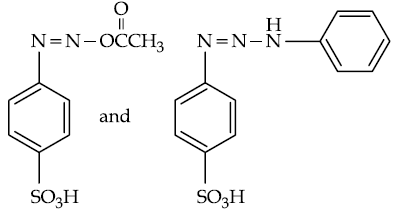
12. Oxidation of toluene to Benzaldehyde can be easily carried out with which of the following reagents?
(A) CrO3/acetic acid, H3O+
(B) CrO3/acetic anhydride, H3O+
(C) KMnO4/HCl, H3O+
(D) CO/HCl, anhydrous AlCl3
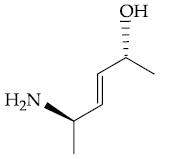
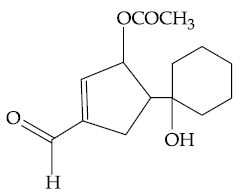
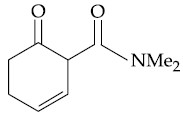
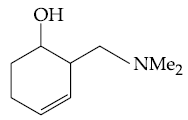
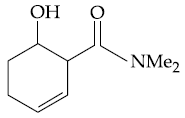
13. The major product in the following reaction
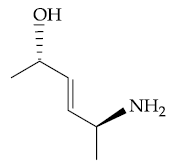
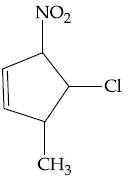
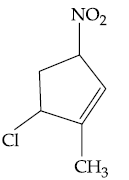
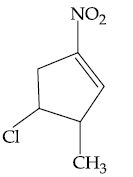
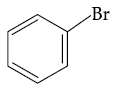
14. Halogenation of which one of the following will yield m-substituted product with respect to methyl group as a major product?
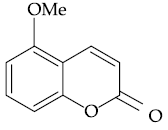
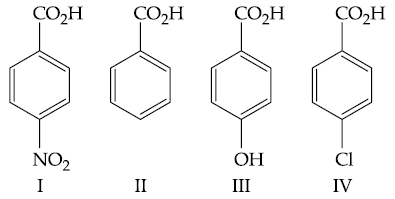
15. The reagent, from the following, which converts benzoic acid to benzaldehyde in one step is
(A) LiAlH4
(B) KMnO4
(C) MnO
(D) NaBH4
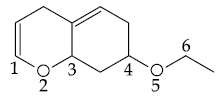
16. The final product ‘A’ in the following reaction sequence
17. Which statement is NOT correct for p-toluenesulphonyl chloride?
(A) It is known as Hinsberg’s reagent
(B) It is used to distinguish primary and secondary amines
(C) On treatment with secondary amine, it leads to a product, that is soluble in alkali
(D) It doesn’t react with tertiary amines
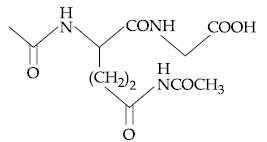
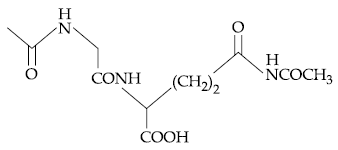
18. The final product ‘C’ in the following series of reactions
19. Which of the following is NOT an example of synthetic detergent?
20. Which one of the following is a water soluble vitamin, that is not excreted easily?
(A) Vitamin B2
(B) Vitamin B1
(C) Vitamin B6
(D) Vitamin B12
SECTION-B
21. CNG is an important transportation fuel. When 100 g CNG is mixed with 208 g oxygen in vehicles, it leads to the formation of CO2 and H2O and produced large quantity of heat during this combustion, then the amount of carbon dioxide, produced in grams is _____. [nearest integer]
22. In a solid AB, A atoms are in ccp arrangement and B atoms occupy all the octahedral sites. If two atoms from the opposite faces are removed, then the resultant stoichiometry of the compound is AxBy. The value of x is ___________. [nearest integer]
23. Amongst SF4, XeF4, CF4 and H2O, the number of species with two lone pair of electrons is _____.
24. A fish swimming in water body when taken out from the water body is covered with a film of water of weight 36 g. When it is subjected to cooking at 100 °C, then the internal energy for vaporization in kJ mol–1 is ________. [nearest integer]
[Assume steam to be an ideal gas. Given ΔvapH⊝ for water at 373 K and 1 bar is 41.1 kJ mol–1; R = 8.31 J K–1mol–1]
25. The osmotic pressure exerted by a solution prepared by dissolving 2.0 g of protein of molar mass 60 kg mol–1 in 200 mL of water at 27°C is _________ Pa. [Integer value]
(use R = 0.083 L bar mol–1 K–1)
26. 40% of HI undergoes decomposition to H2 and I2 at 300 K. ΔG° for this decomposition reaction at one atmosphere pressure is ________ J mol–1. [nearest integer]
(Use R = 8.31 J K–1mol–1; log 2 = 0.3010, ln 10 = 2.3, log 3 = 0.477)
27. Cu(s) + Sn2+ (0.001 M) → Cu2+ (0.01M) + Sn(s) The Gibbs free energy change for the above reaction at 298 K is x × 10–1 kJ mol–1; The value of x is______. [nearest integer]
[Given : F = 96500C mol−1]
28. Catalyst A reduces the activation energy for a reaction by 10 kJ mol–1 at 300 K. The ratio of rate constants, is ex. The value of x is _______. [nearest integer]
[Assume that the pre-exponential factor is same in both the cases.
Given R = 8.31 J K–1mol–1]
29. Reaction of [Co(H2O)6]2+ with excess ammonia and in the presence of oxygen results into a diamagnetic product. Number of electrons present in t2g–orbitals of the product is _______ .
30. The moles of methane required to produce 81 g of water after complete combustion is ______ × 10–2 [nearest integer]
MATHEMATICS
SECTION A
1. Let f : ℝ→ℝ be defined as f(x) = x – 1 and g : ℝ− {1, −1} →ℝ be defined as
Then the function fog is:
(A) One-one but not onto
(B) Onto but not one-one
(C) Both one-one and onto
(D) Neither one-one nor onto
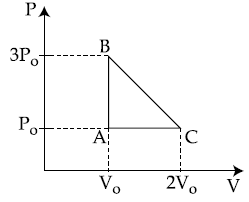
2. If the system of equations αx + y + z = 5, x + 2y + 3z = 4, x + 3y +5z = β has infinitely many solutions, then the ordered pair (α, β) is equal to:
(A) (1, –3)
(B) (–1, 3)
(C) (1, 3)
(D) (–1, –3)
3. If and
then A/B is equal to:
(A) 11/9
(B) 1
(C) −11/9
(D) −11/3
4. is equal to :
(A) 1/3
(B) 1/4
(C) 1/6
(D) 1/12
5. Let f(x) = min {1, 1 + x sin x}, 0 ≤ x ≤ 2π. If m is the number of points, where f is not differentiable, and n is the number of points, where f is not continuous, then the ordered pair (m, n) is equal to
(A) (2, 0)
(B) (1, 0)
(C) (1, 1)
(D) (2, 1)
6. Consider a cuboid of sides 2x, 4x and 5x and a closed hemisphere of radius r. If the sum of their surface areas is a constant k, then the ratio x : r, for which the sum of their volumes is maximum, is
(A) 2 : 5
(B) 19 : 45
(C) 3 : 8
(D) 19 : 15
7. The area of the region bounded by y2 = 8x and y2 = 16(3 – x) is equal to
(A) 32/3
(B) 40/3
(C) 16
(D) 19
8. If g(1) = 0, then g(1/2) is equal to :
9. If y = y(x) is the solution of the differential equation y(1) = 0, then the local maximum value of the function z(x) = x2y(x)-ex, x ∈ R is :
(A) 1 – e
(B) 0
(C) 1/2
(D) 4/e – e
10. If the solution of the differential equation satisfies y(0) = 0, then the value of y(2) is __________.
(A) −1
(B) 1
(C) 0
(D) e
11. If m is the slope of a common tangent to the curves and x2 + y2 = 12, then 12m2 is equal to :
(A) 6
(B) 9
(C) 10
(D) 12
12. The locus of the mid-point of the line segment joining the point (4, 3) and the points on the ellipse x2 + 2y2 = 4 is an ellipse with eccentricity:
(A) √3/2
(B) 1/2√2
(C) 1/√2
(D) 1/2
13. The normal to the hyperbola at the point (8, 3√3) on it passes through the point:
(A) (15, −2√3)
(B) (9, 2√3)
(C) (−1, 9√3)
(D) (−1, 6√3)
14. If the plane 2x + y – 5z = 0 is rotated about its line of intersection with the plane 3x – y + 4z – 7 = 0 by an angle of π/2, then the plane after the rotation passes through the point:
(A) (2, –2, 0)
(B) (–2, 2, 0)
(C) (1, 0, 2)
(D) (–1, 0, –2)
15. If the lines and
are co-planar, then the distance of the plane containing these two lines from the point (α, 0, 0) is :
(A) 2/9
(B) 2/11
(C) 4/11
(D) 2
16. Let and
be three given vectors. Let
be a vector in the plane of
whose projection on
is equal to
(A) 6
(B) 7
(C) 8
(D) 9
17. The mean and standard deviation of 50 observations are 15 and 2 respectively. It was found that one incorrect observation was taken such that the sum of correct and incorrect observations is 70. If the correct mean is 16, then the correct variance is equal to :
(A) 10
(B) 36
(C) 43
(D) 60
18. 16 sin(20°) sin(40°) sin(80°) is equal to :
(A) √3
(B) 2√3
(C) 3
(D) 4√3
19. If the inverse trigonometric functions take principal values, then is equal to:
(A) 0
(B) π/4
(C) π/3
(D) π/6
20. Let r ∈ {p, q, ~p, ~q} be such that the logical statement r ∨ (~p) ⇒ (p ∧ q) ∨ r is a tautology. Then r is equal to :
(A) p
(B) q
(C) ~p
(D) ~q
SECTION-B
21. Let f: ℝ → ℝ satisfy f(x + y) = 2x f(y) + 4y f(x), ∀ x, y ∈ ℝ. If f(2) = 3, then is equal to ___.
22. Let p and q be two real numbers such that p + q = 3 and p4 + q4 = 369. Then is equal to ________.
23. If z2 + z + 1 = 0, z ∈ ℂ, then is equal to ________.
24. Let Y = aI + βX + γX2 and Z = α2I – αβX + (β2 – αγ)X2, α, β, γ ∈ ℝ. If
then (α–β + γ)2 is equal to ___________.
25. The total number of 3-digit numbers, whose greatest common divisor with 36 is 2, is ________
26. If (40C0) + (41C1) + (42C2) + …+(60C20) m and n are coprime, then m + n is equal to _________.
27. If a1 (> 0), a2, a3, a4, a5 are in a G.P., a2 + a4 = 2a3 + 1 and 3a2 + a3 = 2a4, then a2 + a4 + 2a5 is equal to _______.
28. If integral is equal to _______.
29. Let a line L1 be tangent to the hyperbola and let L2 be the line passing through the origin and perpendicular to L1. If the locus of the point of intersection of L1 and L2 is (x2 + y2)2 = αx2 + βy2, then α + β is equal to _________.
30. If the probability that a randomly chosen 6-digit number formed by using digits 1 and 8 only is a multiple of 21 is p, then 96 p is equal to ________.
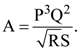
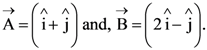 The magnitude of a coplanar vector
The magnitude of a coplanar vector 
 for the mixture, then the value of n is :
for the mixture, then the value of n is :


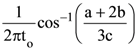
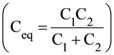
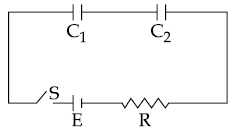

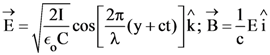
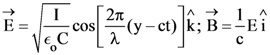
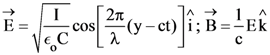
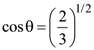
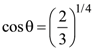






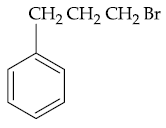
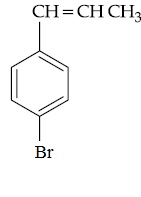
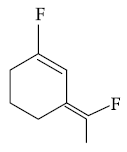




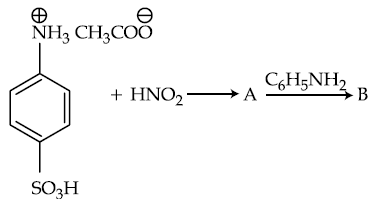













 is
is and B = A20. Then the sum of the elements of the first column of B is :
and B = A20. Then the sum of the elements of the first column of B is :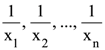 (xi ≠ 2 for i = 1, 2, . . . , n) be in A.P. such that x1 = 4 and x21 = 20. If n is the least positive integer for which xn > 50, then
(xi ≠ 2 for i = 1, 2, . . . , n) be in A.P. such that x1 = 4 and x21 = 20. If n is the least positive integer for which xn > 50, then 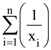 is equal to :
is equal to :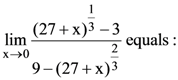






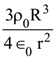
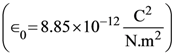

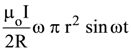


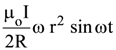
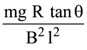


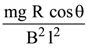
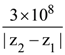
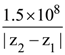

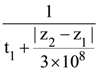



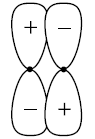










 and Bn = 1 – An. Then, the least odd natural number p, so that Bn > An, for all n ≥ p, is :
and Bn = 1 – An. Then, the least odd natural number p, so that Bn > An, for all n ≥ p, is :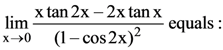
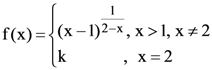
 equals :
equals :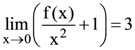 then f(−1) is equal to :
then f(−1) is equal to :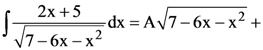

 is :
is :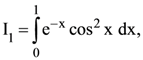
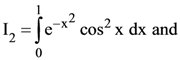
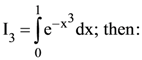


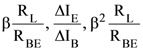
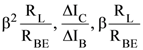



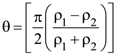
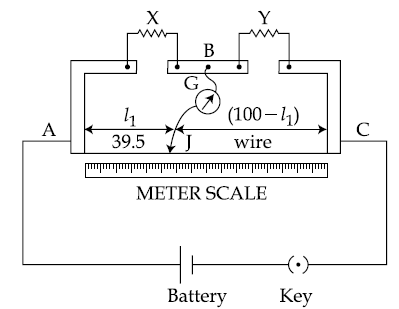
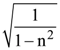

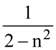


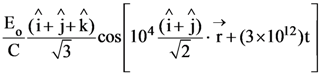



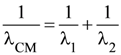












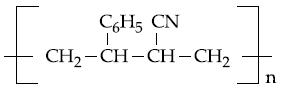
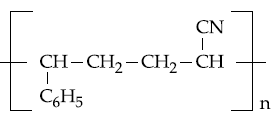
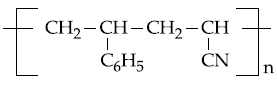
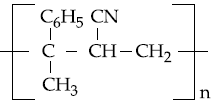
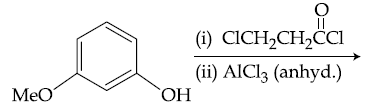

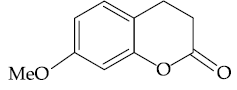
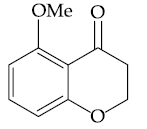






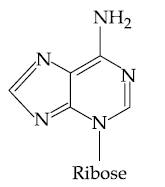
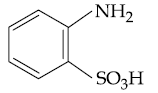
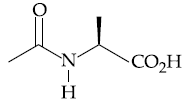


 are two A.P.s such that x3 = h2 = 8 and x8 = h7 = 20, then x5∙h10 equals :
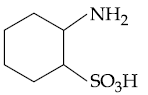
are two A.P.s such that x3 = h2 = 8 and x8 = h7 = 20, then x5∙h10 equals :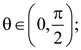 then
then 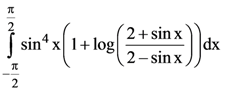 is :
is :
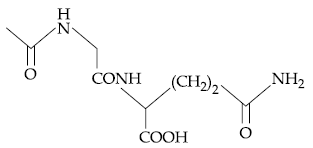
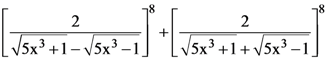 and m is the coefficient of xn in it, then the ordered pair (n, m) is equal to :
and m is the coefficient of xn in it, then the ordered pair (n, m) is equal to : is a scalar matrix and |3A| = 108. Then A2 equals :
is a scalar matrix and |3A| = 108. Then A2 equals :
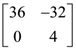
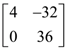

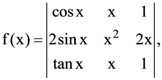 then
then 




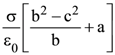

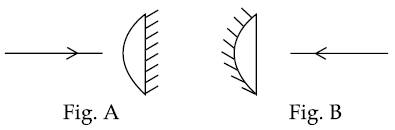
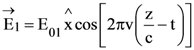 in air and
in air and 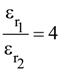
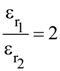


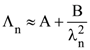



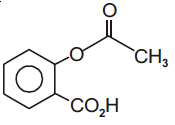
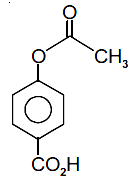

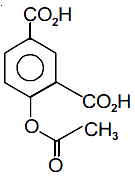

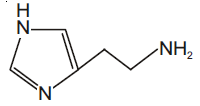

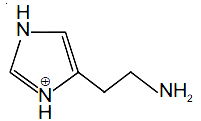
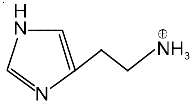

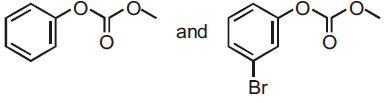

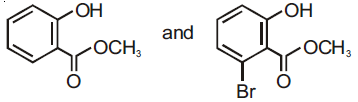

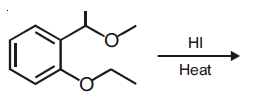
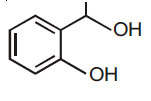

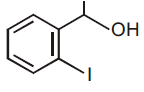

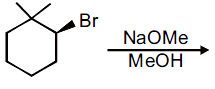
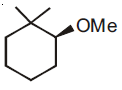
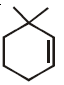
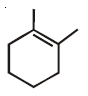

 then the ordered pair (A, B) is equal to
then the ordered pair (A, B) is equal to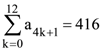 and a9 + a43 = 66.
and a9 + a43 = 66.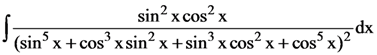 is equal to
is equal to is :
is : then the standard deviation of the 9 items x1, x2, …. ., x9 is
then the standard deviation of the 9 items x1, x2, …. ., x9 is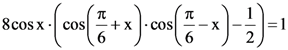 in [0, π] is kπ, then k is equal to :
in [0, π] is kπ, then k is equal to :